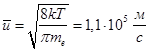Dependence of the resistance of the conductor of temperature. Superconductors. Elementary classical theory of electrical conductivity of metals. Work and power of current. Joule-Lenz law. Kirchoff's law for branched chain.

main

To the list of lectures

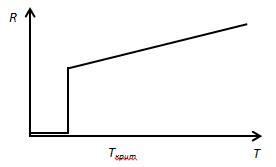
§ 3. Dependence of the resistance the conductor temperature. Superconductors

With increasing temperature, the resistance of the conductor increases linearly

where R₀ - resistance at t = 0° C; R-resistance at temperature t, α - coefficient of thermal resistance, shows how changing resistance of a conductor temperature changes by 1 degree . For pure metals at not too low temperatures , ie, we can write

At a certain temperature (0,14-20 K), called the "critical" conductor resistance sharply reduced to 0 and the metal becomes superconducting. For the first time in 1911, it discovered Kamerlingh Onnes for mercury. In 1987 the designed ceramics, passing into the superconducting state at temperatures above 100 K, the so-called high-temperature superconductors - HTS.

§ 4 The elementary classical theory of electrical conductivity of metals

$Описание: C:\Users\AP\AppData\Local\Temp\FineReader11\media\image2.jpeg$

Carriers in metals are free electrons, ie weakly bound electrons with ions of the crystal lattice of the metal. The presence of free electrons explained by that the formation of the crystal lattice of the metal during the approach of isolated atoms, valence electrons are weakly coupled with atomic nuclei, break away from the metal atom to become "free" socialized belonging not to an individual atom and the whole matter, and can move on throughout. In the classical electron theory, these electrons are treated as an electron gas with the properties of a monatomic ideal gas.

Conduction electrons in absence of an electric field inside the metal randomly move and collide with the ions of the crystal lattice of the metal. Thermal motion of the electrons, being chaotic, can not give rise to current. Average thermal velocity of the electrons

при Т = 300 К.

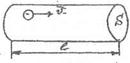
2. The electric current in the metal arises under influence of an external electric field, which causes the orderly movement of electrons. Express the current intensity and the current density of the velocity v of the ordered motion of electrons in a conductor.

$Описание: C:\Users\AP\AppData\Local\Temp\FineReader11\media\image3.jpeg$ During the time dt through the cross section S of the conductor will be N electrons

, ;

therefore, even at very high current densities, the average velocity of the ordered motion of electrons , causes the electric current is much smaller than the speed of thermal motion .

The electric current in the circuit is set in a time , where the L-

chain length , с = 3·10⁸ m/s - the speed of light in vacuum. The electric current in the circuit disappear almost simultaneously with its closure.

The mean free path of the electrons of the order of λ must be equal to the period of the crystal lattice of the met λ @ 10^-10 м.
With increasing temperature, increasing the amplitude of oscillation of the crystal lattice of ions and electron bowl facing fluctuating ions, so it decreases the mean free path, and the resistance of the metal increases.

Shortcomings of the classical theory of electrical conductivity of metals:

1. (1)

because~ , n and λ ≠ f(T) ρ ~ ,

ie from the classical theory of electrical conductivity, the specific resistance is proportional to the square root of the temperature, and from experience that it is linearly dependent on the temperature, ρ ~ Т

2. Gives an incorrect value of the molar heat capacity of metals. According to the law of Dulong and Petit С_μ = 3R,and the classical theory of С = 9 / 2R=C_μ _{ionic lattice} = 3R + C_{μ monatomic electron gas} = 3/2R.

3. The mean free path of electrons from (1) by substituting the experimental value ρ and the theoretical value of gives 10^-8, which is two orders of magnitude larger than the mean free path assumed in the theory (10^-10).

§ 5. Work and power supply. Joule-Lenz’s law

Because charge is transferred to the conductor under the influence of the electrostatic field, his work is

Power - the work done per unit of time

[P] = W (watts).

If the current is a stationary conductor, the entire current work goes into heating the metal conductor, and the law of conservation of energy

Joule-Lenz;s law.

Specific power current is the amount of heat per unit volume emitted a conductor per unit time.

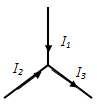
Joule--Lenz 's law in differential form.

§ 5 Kirchhoff's rules for the branched chain

Any point of the branched chain, which converges at least three conductors a current, is called a node. In this talk, part of the node is positive, and going out – no.

The first rule of Kirchhoff: algebraic sum of the currents that converge at a node is equal to zero

Kirchhoff's first rule follows from the law of conservation of charge (the charge, who entered to the node is the withdrawing charge).
The second rule of Kirchhoff: in any closed loop randomly chosen in a branched circuit, the algebraic sum of the products of forces of current to resistance relevant sections of this circuit is equal to the algebraic sum of the EMF. occurring in the circuit.

In the calculation of complex direct current circuits using Kirchhoff's rules should:
1. Choose an arbitrary direction of the currents at all stages of the chain, the actual direction of the currents is determined to solve the problem, if desired current is turned positive, the direction is right, if negative, the opposite of its true direction chosen.

2. Choose the direction of the circuit. Product

is positive when the current at the site coincides with the direction of passage, and vice versa. EMF positive if they produce a current directed towards the contour - against negative.

3. Recorded the first rule to N -1 node.

4. Write the second Kirchhoff's rules for closed loops that can be allocated in the chain. Each considered circuit must contain at least one element that is not contained in the previous circuits.
The number of independent equations, but in accordance with the first and second rule of Kirchhoff, is equal to the number of different currents in the branched chain. Therefore, given the EMF and resistance to all areas of unbranched, it can be calculated all the currents.