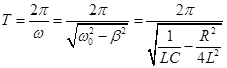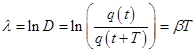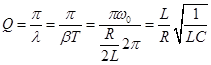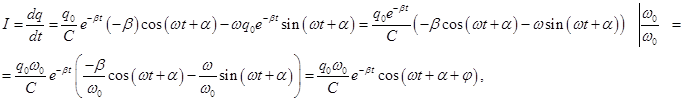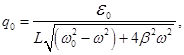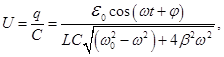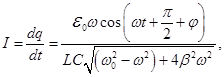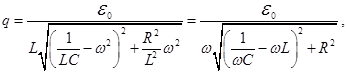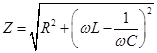|
Electromagnetic Oscillations and Waves
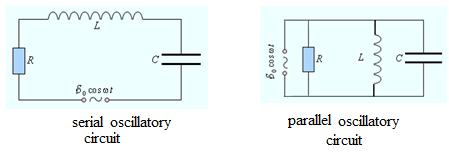
§ 1 of the resonant circuit.
The natural oscillations in resonant circuit.
Thomson formula.
Damped and forced oscillations r. c.
- Free oscillations in r.c.
Oscillating circuit (R.C.) is a
chain consisting of capacitors and inductors. Under certain conditions
r. c. can cause electromagnetic oscillations of the charge, current,
voltage and power.
Consider the
circuit shown in Figure 2. If you put the key in position 1, there will
be a charge on the capacitor and its plates will charge Q and voltage
UC. If you then put the key in position 2, 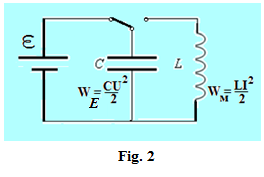 the
capacitor will discharge, a current will flow in the circuit, and the
energy of the electric field between the plates of a capacitor, will be
transformed into the energy of the magnetic field is concentrated in
the inductor L. The presence of the inductor causes the current in the
circuit increases, not immediately, but gradually due to the
phenomenon of self-induction. As the discharge of the capacitor charge
on its plates will be reduced, the current in the circuit to
increase. Maximum loop current to reach at a charge equal to zero on
the plates. Since then loop current will begin to decrease, but, due to
the phenomenon of self-induction, it will be supported by the magnetic
field of the coil, ie at full capacitor discharge magnetic energy
stored in the inductor, the energy will go into the electric field.
Because of the loop current will begin recharging the capacitor and its
plates will accumulate a charge opposite to the original. Recharging
of the capacitor will be long until the power of the magnetic field
coil goes into the energy of the electric field condenser. The process
is then repeated in the opposite direction, and, thus, in the chain of
any electromagnetic vibrations. the
capacitor will discharge, a current will flow in the circuit, and the
energy of the electric field between the plates of a capacitor, will be
transformed into the energy of the magnetic field is concentrated in
the inductor L. The presence of the inductor causes the current in the
circuit increases, not immediately, but gradually due to the
phenomenon of self-induction. As the discharge of the capacitor charge
on its plates will be reduced, the current in the circuit to
increase. Maximum loop current to reach at a charge equal to zero on
the plates. Since then loop current will begin to decrease, but, due to
the phenomenon of self-induction, it will be supported by the magnetic
field of the coil, ie at full capacitor discharge magnetic energy
stored in the inductor, the energy will go into the electric field.
Because of the loop current will begin recharging the capacitor and its
plates will accumulate a charge opposite to the original. Recharging
of the capacitor will be long until the power of the magnetic field
coil goes into the energy of the electric field condenser. The process
is then repeated in the opposite direction, and, thus, in the chain of
any electromagnetic vibrations.
We write the 2nd Kirchoff's considered r.c.
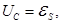
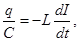
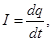
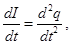
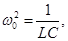
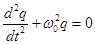
- Differential equation R.C.
We obtain the differential
equation for the oscillations of charge r. c. This equation is
similar to the differential equation describing the motion of a body
under the quasi-elastic force. Therefore, will likewise be recorded and solution of this equation
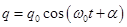
- The equation of charge oscillations r. c.

- Equation of voltage fluctuations on the capacitor plates r. c.

- Equation of the current oscillations r. c.
2. Damped oscillations r. c.
Consider the R.C. containing capacitance, inductance and resistance. 2nd Kirchhoff's law in this case is written as
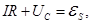
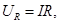
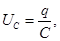
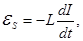
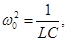
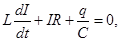
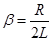 - damping factor , - damping factor ,
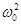 - own cyclic frequency . - own cyclic frequency .

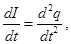
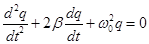
-differential equation of damped oscillations r. c.
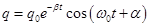
- equation of damped oscillations of the charge r. c.
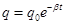
- law of variation of the amplitude of the charge for the damped oscillations in the R.C.:
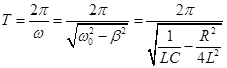
- The period of the damped oscillations .
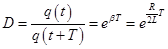
- damping rate .
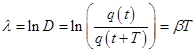
- logarithmic damping decrement.
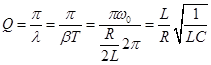
- quality factor of the circuit .
If 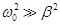 the damping is weak, then Т ≈Т0 the damping is weak, then Т ≈Т0
Investigate the change in the voltage on the capacitor plates.
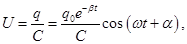
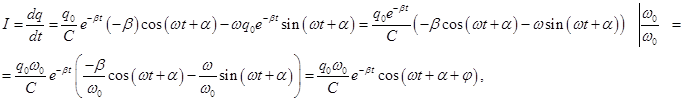
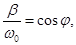
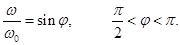
Current change is different in phase φ of the voltage.
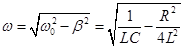
at 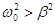 - possible damped oscillations, - possible damped oscillations,
at 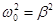 -emergency -emergency
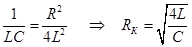
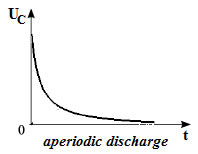
at 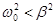 , ie R > RК – , ie R > RК –
fluctuations do not occur (aperiodic discharge capacitor).
3. forced oscillations
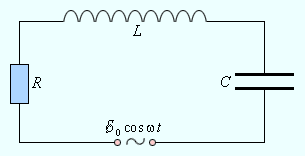 Undamped
electromagnetic oscillations will occur in r. c. containing R, L and C
in the case in this circuit to enter the EMF varies as a sine or
cosine. In the circuit after the time of formation of forced
oscillations occur undamped electromagnetic waves with frequency of
the driving force. Undamped
electromagnetic oscillations will occur in r. c. containing R, L and C
in the case in this circuit to enter the EMF varies as a sine or
cosine. In the circuit after the time of formation of forced
oscillations occur undamped electromagnetic waves with frequency of
the driving force.
Apply the 2nd Kirchhoff's law to the subject R.C.

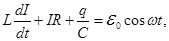
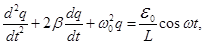
ω –the frequency of the driving force
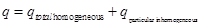

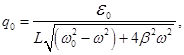
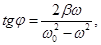
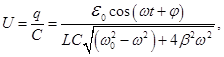
The law of change current
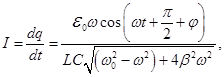 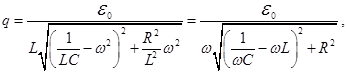
The law of change charge
- Impedance.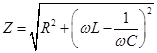

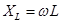 - Inductance. - Inductance.
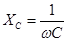 - Capacitance. - Capacitance.
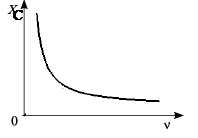
|