§ 6 Entropy

Usually, any process in which the system moves from one state to another, occurs in a way that can not be done this process in the opposite direction so that the system passed through the same intermediate states, while in others the bodies are not any changes. This is due to the fact that in the process of the energy is dissipated, for example, due to friction, radiation, etc. Thus. almost all processes in nature are irreversible. In any process of the energy is lost. To characterize the energy dissipation is introduced the concept of entropy. (The entropy characterizes the thermal state of the system and determines the probability of a given state of the body. The more likely this condition, the greater the entropy.) All natural processes are accompanied by an increase in entropy. Entropy is constant only in the case of an idealized reversible process that occurs in a closed system, ie a system in which there is an exchange of energy with the external to this system bodies.

Thermodynamic entropy and its meaning:

Entropy - is a function of the system, an infinitesimal change in a reversible process which is the ratio of the infinitesimal amount of heat introduced into the process, to the temperature at which it was introduced.

All in a reversible process the entropy change can be calculated by the formula:

where the integration is one of the initial state 1 of the system to the final state 2.
Since entropy is a state function, the integral  is the property of its independence from the shape of the contour (path), on which it is calculated, so the integral is determined only by the initial and final states of the system.

In any reversible process the change in entropy is equal to 0

                       (1)

2) In thermodynamics, it is proved that the system undergoes irreversible S cycle increases

ΔS> 0 (2)

Equations (1) and (2) apply only to closed systems, but if the system is exchanged heat with the environment, its S can behave in any way.

Of (1) and (2) can be written as the Clausius inequality

ΔS ≥ 0

ie entropy of a closed system can either increase (in the case of irreversible processes) or remain constant (in the case of reversible processes).

If the system performs the equilibrium transition from state 1 to state 2, the entropy change

where dU and δA is recorded for a particular process. According to this formula ΔS is determined up to an additive constant. The physical meaning is not the entropy, entropy difference. We find the entropy change in the process of an ideal gas.

ie changes in the entropy S ΔS_{1 → 2}  ideal gas at its transition from state 1 to state 2 is independent of the process.

Because for an adiabatic process δQ = 0, ΔS = 0 => S = const, ie adiabatic reversible process takes place at constant entropy. So it is called isentropic.

An isothermal process (T = const;  T₁ = T₂:   )

When isochoric process (V = const; V₁ =V₂;  )

Entropy is additive: the entropy of the system is the sum of the entropies of bodies in the system. S = S₁ + S₂ + S₃ + ... Qualitative difference of the thermal motion of molecules from other forms of movement is its state of chaos, randomness. Therefore, to characterize the thermal motion to introduce a quantitative measure of the degree of molecular disorder. If we consider any given macroscopic state of the body with some average values, then it is nothing but the continuous change of close microstates differing distribution of molecules in different parts of the volume and the energy is distributed between the molecules. These continuous successive microstates characterizes the degree of disorder of the macroscopic state of the entire system, ϖ is called thermodynamic probability of the microstate. Thermodynamic probability ϖ of the system - is the number of ways that this can be done state macroscopic system, or the number of microstates carrying this microstate (ϖ ≥ 1, and the mathematical probability of ≤ 1).
As a measure of unexpected events have agreed to take the logarithm of its probability, the negative of: unexpected state is = - ln ? ω

According to Boltzmann, the entropy S of the system and the thermodynamic probability linked as follows:

where k - Boltzmann constant, . Thus, the entropy is defined logarithm of the state in which this can be achieved microstate. Entropy can be considered as a measure of the probability of the state thermodynamic system. Boltzmann formula allows us to give the following statistical interpretation of entropy. Entropy is a measure of disorder in a system. In fact, the greater the number of microstates realizing this microstate, the greater the entropy. In the equilibrium state of the system - the most probable state of the system - the maximum number of microstates, with the maximum and entropy.

Because real processes are irreversible, it can be argued that all the processes in a closed system leads to an increase in its entropy - the principle of entropy increase. In the statistical interpretation of entropy, this means that the process in a closed system are to increase the number of microstates, in other words, from less probable to more probable, as long as the probability of the state will not be maximized.

§7 The second law of thermodynamics

The first law of thermodynamics, expressing energy conservation and transformation of energy, does not establish the direction of the flow thermodynamic processes. You can also submit a set of processes that do not contradict the beginning I law thermodynamic, in which energy is conserved, but in nature they are not implemented. Possible formulation of the second law of thermodynamics:
1) the law of increasing entropy of a closed system in irreversible processes: any irreversible process in a closed system is such that the entropy of the system is on the increase ΔS ≥ 0 (irreversible)

2) ΔS ≥ 0 (S = 0 for a reversible and ΔS ≥ 0 for an irreversible process)
The processes that take place in a closed system, entropy does not decrease.
2) From the Boltzmann S = k ln ω > 0, and consequently, an increase in the entropy of the system means the transition from a less probable to a more probable state.

3) According to Kelvin: circular process is not possible, the only result of which is the conversion of heat received from the heater into an equivalent work.

4) In the Clausius: circular process is not possible, the only result is to transfer heat from the less heated body to a warmer.

To describe the thermodynamic systems at 0 K using Theorem Nernst-Planck (third thermodynamics): the entropy of all bodies in equilibrium tends to zero as the temperature approaches 0 K

From Theorem Nernst-Planck equation, it follows that C_p = C_v = 0 at 0 K.

§ 8 Thermal and refrigerators.

Carnot cycle and its efficiency

From the wording of the second law of thermodynamics on  Kelvin that a perpetual motion machine of the second kind is impossible. (Perpetual motion - this batch engine does work by cooling a heat source.)

Thermostat - is thermodynamic system that can exchange heat with the bodies without a change in temperature.

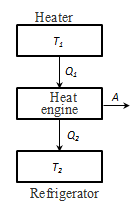
The principle of operation of the heat engine: the thermostat with temperature T₁ - heater for a cycle is subtracted the amount of heat Q₁, a thermostat with temperature T₂ (T₂ < T₁), refrigerator, for a series of heat transferred to Q₂, while work is done A = Q₁ - Q₂

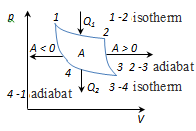
Circular process or cycle is a process by which the system is going through a number of states, is reset. Cycle in the state diagram depicted a closed curve. Cycle, performed by an ideal gas can be divided into processes of expansion (1-2) and compression (2-1), the work of expansion is positive A_1-2 > 0, because V₂> V₁, the work of compression is negative A_1-2 < 0, because V₂ < V₁. Hence, the work done by the gas per cycle, determined by the area covered by a closed curve 1-2-1. If the cycle is done positive work   loop clockwise), then the cycle is called direct if - reverse cycle (cycle occurs in a counter-clockwise).
Direct cycle is used in heat engines - periodically a motor does the work by producing heat from the outside. Reverse cycle is used in refrigerators - periodically existing installations, in which through the work of external forces, heat is transferred to the body with a higher temperature.
As a result of the circular process, the system returns to its initial state, and therefore, the total change in internal energy is zero. Then start the I law of thermodynamics for a circular process

that is, the work done per cycle is the amount of heat received from the outside, but

Q = Q1 - Q2

Q₁ - the amount of heat received by the system

Q₂ - the amount of heat given system.

Thermal efficiency for cyclic process is the ratio of the work done by the system, to the amount of heat supplied to the system:

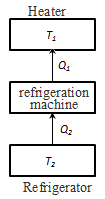
To η = 1, the condition Q₂ = 0, ie, heat engine should have one heat source Q₁, but this contradicts the second law of thermodynamics.

The reverse process is happening in the heat engine is used in the refrigeration machine.

The thermostat with temperature Т₂ deducted the amount of heat Q₂ transferred to the thermostat and the temperature T₁, the amount of heat Q₁.
Q = Q₂ - Q₁ < 0 so A < 0.

Without doing the work can not take away the heat from a hot body, and at least give it a warmer.

Based on the second law of thermodynamics, Carnot led theorem.
Carnot's theorem: From time to time all heat engines operating with the same heater temperature (T₁) and refrigerators (T₂), the highest efficiency have a reversible machine. Efficiency reversible machine with equal T₁ and T₂ are equal and do not depend on the nature of the working fluid.

Working body - the body to make circular process to exchange energy to other bodies.
Carnot cycle - the most economical reversible cycle consisting of 2 isotherms and 2 adiabats.

1-2-isothermal expansion at T₁ heater, gas is supplied to the heat Q₁ and work is done

2 - 3 - adiabats. expansion, the gas does work A_2-3 > 0 on external bodies.

3 - 4-isothermal compression at T₂ refrigerator, heat is taken Q₂ and work is done

4-1-adiabatic compression work is done on the gas A_4-1 < 0 external bodies.
An isothermal process U = const, so Q₁ = A₁₂

Adiabatic expansion Q_2-3 = 0, and the work done A₂₃ gas by the internal energy A₂₃ = -U

The amount of heat Q₂, uploaded from gas to refrigerator at isothermal compression equal to the work of compression А_3-4

The work of the adiabatic compression

The work performed by a circular process

and equal to the area of ??the curve 1-2-3-4-1.

Thermal efficiency Carnot cycle

From the equation for adiabatic processes 2-3 and 3-4 we obtain

then

ie efficiency Carnot cycle is determined only by the temperature heater and refrigerator. To increase the efficiency necessary to increase the difference Т₁ - Т₂.