|
§4 I law of thermodynamics, Q, U, A to izoprocesses
- Isothermal process T = const, m = const.
Boyle's law
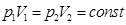
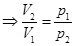
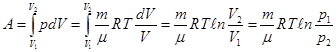
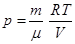

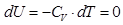
 
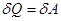
ie the total amount of heat imparted to the gas is consumed in the performance of his work against external forces
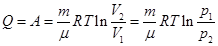
that
at work expanding the temperature did not change to gas during the
isothermal process is necessary to sum up the amount of heat equivalent
to the work of foreign expansion.
- Isobaric process. p = const m = const
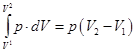

Of Mendeleev-Clapeyron equation for state 1 and 2:
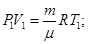
 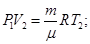
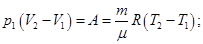
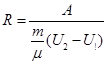
The physical meaning of R: R is numerically equal to the work by heating 1 mole of gas at 1K (T2 - T1 = 1 K) in the isobaric process.
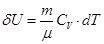 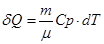

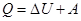
heat supplied to the gas, is the change in its internal energy and the work of the commission
- Isochoric process
V = const, m = const
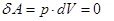
because 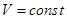
and
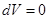
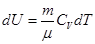 


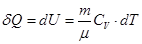
All the warmth imparted by gas, is the change in its internal energy.
§ 5 The adiabatic process.
Polytropic process
Called adiabatic process that takes place without heat exchange with the environment. To
include all the adiabatic fast processes. For example, an adiabatic process can be regarded as
the
propagation of sound in the medium, as speed of sound is so high that
the energy exchange between the wave and the medium does not have time
to happen. Adiabatic processes are used in internal combustion engines,
refrigeration, etc. We find the equation relating the parameters of
ideal gas at an adiabatic process.
We write I law of thermodynamics.
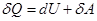
For an adiabatic process
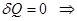
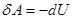
ie external work is done by changing the internal energy of the system
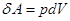

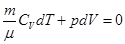
From equation Mendeleev-Clapeyron express p
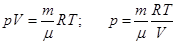
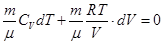
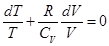
Rewritten as:
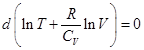
Ie

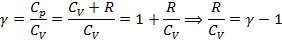
Potentiated
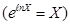
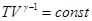
- Adiabatic equation in the coordinates T and V.
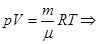
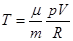

- The Poisson equation (adiabatic equation in the coordinates p and V):

 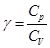 - the adiabatic (or Poisson's ratio). - the adiabatic (or Poisson's ratio).
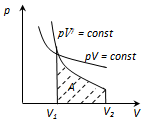
pV = const - isotherm equation as γ
> 1, the adiabatic curve is steeper than the isotherm. This is
explained by the fact that the adiabatic compression 1 - 3 increase in
gas pressure due not only to a decrease in its volume as an isothermal
compression, but also increase in temperature
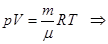


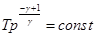
- adiabatic equation in the coordinates p, T.
Compute the work is done by the gas in an adiabatic process.
I law of thermodynamics for an adiabatic process
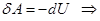
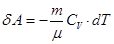
If the gas adiabatically expands from volume V1 to V2, its temperature decreases from T1 to T2, and the work of expansion of ideal gas
 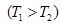
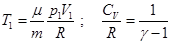

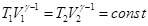
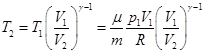
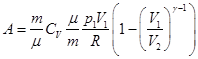
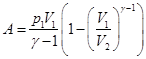
The
work done by the gas during the adiabatic expansion 1- 2 is
equal to square, shaded in the figure and it is less than the work of
an isothermal expansion. This is explained by the fact that the
adiabatic expansion cools the gas, whereas the isothermal expansion
temperature is kept constant by the influx from the outside of the
equivalent amount of heat.
Considered isochoric, isobaric, isothermal and adiabatic processes have in common - they occur at constant heat capacity (CV, CP, CT = ∞, CA = 0). In the first two processes are equal to the heat capacity Cv and Cp in an isothermal process (dT = 0) CT = ∞, in an adiabatic process δQ = 0 and CA = 0.
The process in which heat is constant is called polytropic (C = const). Started on the basis of I law thermodynamics at a constant heat capacity (C = const) can be derived polytropic equation
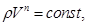
where
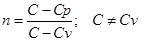
n - adiabatic index.
When C = 0 n = γ pvγ=const adiabatic equation
When C = ∞ n = 1 pV = const - isotherm equation
When С = Ср n = 0 p = const, 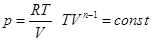
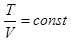 isobar equation isobar equation
When С = СV n = ± ∞ 
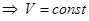
Thus, all the processes are special cases of a polytropic process.
|