main
To the list of lectures
|
ELEMENTS OF QUANTUM MECHANICS In 1924 Louis de Broglie (French physicist) concluded that the duality of light should be extended to particles of matter - electrons. De Broglie's hypothesis was the fact that the electron which the corpuscular properties (charge, mass) are studied for a long time, has also wave properties, ie under certain conditions behaves like a wave. Quantitative relations between the corpuscular and wave properties of particles, such as for photons.
De Broglie's idea was, that this relationship is universal, valid for all wave processes. Any particle that has momentum p corresponds to the wave length of which is given by de Broglie.
p =mv- momentum of the particle, h - Planck constant. De Broglie waves, which are sometimes called electron waves are not electromagnetic.
Macroscopic body must also have all the properties of (m = 1 kg, therefore, l = 6.62·10-31 m - can not be detected by modern methods - so macrobody considered only as corpuscles).
§ 2 Properties of de Broglie wave
Because c > v then the phase velocity of the de Broglie waves faster than light in a vacuum ( vph could be more and could be less then с, as opposed to group). Group velocity
2. therefore, the group velocity of the de Broglie waves equal to the speed of the particle.
i.e. the group velocity is equal to the speed of light.
§3 of the Heisenberg uncertainty relation Microparticles in some cases behave as waves, as in other corpuscles. They do not apply the laws of classical physics, particles and waves. In quantum physics, it is proved that the microparticle can not apply the concept of the path, but we can say that the particle is in a given volume of space with some probability P. Reducing the volume, we will reduce the probability of finding the particle in it. Probabilistic description of the path (or position) of the particle leads to the fact that the momentum and, consequently, the speed of the particle can be determined with a certain accuracy.
Further, it is impossible to speak of a wavelength at a given point,
and it follows that if we are just given the coordinates of X, then there is nothing we can say about the momentum of the particle, because Heisenberg uncertainty relation sets a limit to the simultaneous determination of the accuracy of the canonically conjugate variables, which include the position and momentum, energy and time. Heisenberg uncertainty relation: the product of two conjugate values ??uncertainties quantities can not be in the order of magnitude less than the Planck constant h
(sometimes written
So. for microparticles no states in which its position and momentum at the same time would have the exact values. The smaller the uncertainty of one value, the greater the uncertainty of the other. The uncertainty relation is the quantum limit the applicability of classical mechanics to microobjects.
The larger m, the smaller the uncertainty in determining the position and velocity. at m = 10-12 kg, ℓ = 10-6 and Δx = 1% ℓ, Δv = 6,62·10-14 m/s, i.e. will have no effect at all speeds, with which dust can move, i.e. armatures for their wave properties do not play a role Let the electron moves in a hydrogen atom. Assume Δx»10-10 m (about the size of an atom, i.e., the electron belongs to a given atom). Then Δv = 7,27·106 m/s. According to classical mechanics, the motion of the radius r » 0,5·10-10 m; v = 2,3·10-6 m/s. I.e. velocity uncertainty on the order of magnitude more speed, therefore, can not apply the laws of classical mechanics to the microworld. From relation § 4 The wave function and its physical meaning The
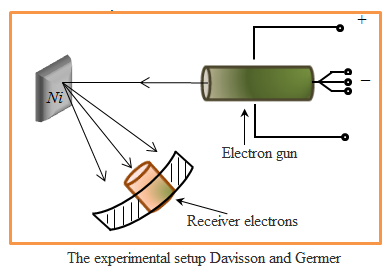
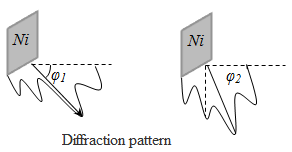
diffraction patterns observed for microparticles, characterized the
unequal distribution of particulate flows in different directions -
there are minimum and maximum in the other direction. The presence of
peaks in the diffraction pattern indicates that these lines are
distributed de Broglie wave with the greatest intensity. But the
intensity will be maximum if in this direction extends the maximum
number of particles. I.e. diffraction pattern for microparticles is a
manifestation of the statistical (probabilistic) laws in the
distribution of particles, where the intensity of the de Broglie wave
maximum out there and more particles. The wave function - a function of position and time. The square modulus of the psi-function gives the probability that a particle will be found within the scope of volume dV - physical meaning not the psi function but the square of its modulus.
Ψ* - function of the complex conjugate to Ψ (z = a +ib, z* =a- ib, z*- complex conjugate) If a particle is in a finite volume V, then the ability to detect it in this volume is equal to 1 (a certain event) Р = 1 ⇒ In quantum mechanics, it is assumed that Ψ and AΨ, where A = const, describe the same state of the particle. Consequently, the
- normalization condition integral, y - function should be 1) final (as P can not be greater than 1) 2) unique (you can not find a particle under constant conditions with a probability of say 0.01 and 0.9, as the probability to be unique). 3)
continuous (from the continuity of space. Always a probability of
finding the particle at different points in space, but at different
points, it will be different)
Сn (n=1,2...) - any number of. With the wave function calculates the average value of any physical quantity of a particle
§ 5 The Schrödinger equation Schrödinger equation, as well as other basic equations of physics (Newton's equations, Maxwell), not outputed, and is postulated. It should be seen as a starting basic assumption, the validity of which is proved by the fact that all the consequences arising out of it exactly in agreement with the experimental data.
- Temporary Schrödinger equation.
Ψ(y, z, t) - unknown function
Е - the total energy of the particle, a constant in a stationary field.
- Schrödinger equation for stationary states.
§ 6 The motion of a free particle
Schrödinger equation for the stationary states in the cases е:
His solution: Ψ(x)=Ае ikx , where А = const, k = const And energy eigenvalues:
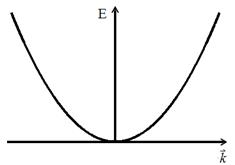
Because k can take any value, then, consequently, E, take any value, i.e. energy spectrum is continuous.
I.e. is flat monochrome de Broglie waves. §7 A particle in the "potential well" rectangular. Quantization of energy. We find the energy eigenvalues ??and the corresponding eigenfunctions for a particle in a one-dimensional infinitely deep potential well. Suppose that the particle can move only along the axis x. Let the motion of the particles is limited impenetrable walls x = 0 and x = ℓ. The potential energy U is:
Schrödinger equation for the stationary states for one-dimensional problem
Potential well beyond the particle will not be able to get, so the probability of finding a particle outside the well is 0. Consequently, Ψ outside the well is 0. From the continuity conditions that Ψ = 0 and on the borders of well that is Ψ(0) = Ψ(ℓ) = 0 Within well (0 ≤ x≤ ℓ) U = 0 and the Schrödinger equation.
by typing General solution
from the boundary conditions follows y(0) = 0, so В = 0 Therefore,
From the boundary condition
Follows
Then
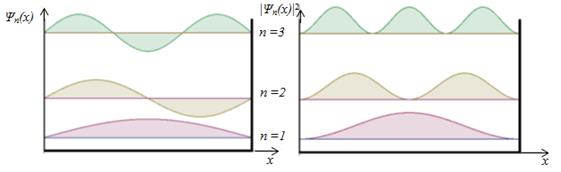
The energy of the particles of En in "potential well" with infinitely high walls accepts only certain discrete values, i.e. quantized. Quantized energies of En called energy levels, and the number n, indicating energetic levels of a particle, called the principal quantum number. I.e. particles in a "potential well" can only be a certain energy level En (or are in the quantum state n) Eigenfunctions: А found from the normalization condition
The energy spacing between adjacent energy levels:
When n = 1 has the lowest energy non-zero
There is a minimum energy follows from the uncertainty principle, because
With increases n the distance between the levels decreases when n→ ∞ Еn almost continuous, i.e. discontinuity is smoothed, i.e. Bohr's correspondence principle holds: for large values ??of the quantum numbers of the laws of quantum mechanics become the laws of classical physics.
§8 The tunnel effect.
Potential energy :
Schrodinger equation for region 1 and 3:
for region 2: The solution of these differential equations: For 1; For 2; For 3: Temporary wave function for the area 1:
Because in region 3 is possible of distribution only of transmitted wave, then, ⇒, В3=0. In region 2, the solution depends on the ratio of Е> U or Е< U. interest is the case Е< U. q = ib, where Then the solution of the Schrödinger equation can be written as: For 1; For 2; For 3: The qualitative form of the functions shown in Fig. 2. From Fig. 2 shows that the function is not zero inside the barrier, and in 3 of the form de Broglie waves, if the barrier is not very wide.
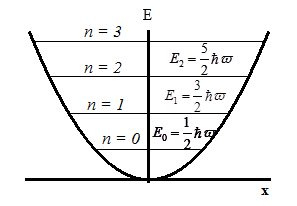
§ 9 The linear harmonic oscillator
Linear harmonic oscillator - the system, to perform a one-dimensional oscillatory motion by quasielastic force - is a model for the study of the vibrational motion. In classical physics - it's spring, physical and mathematical pendulum. In quantum physics - quantum oscillator. Writing the potential energy in the form of
Schrödinger equation can be written as:
Then the energy eigenvalues:
i.e. the energy of a quantum oscillator takes discrete values, i.e. quantized. The minimum value The presence of
zero-point means that the particles can not fall to the bottom of well,
as the in this case would be precisely determined its momentum p = 0, Dp = 0, ⇒, Dx = ∞ - does not match the uncertainty relation. The presence of zero-point energy contradicts |
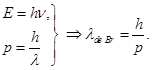
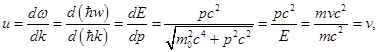
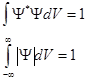
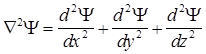
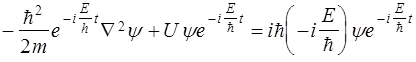
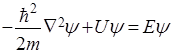
 (3)
(3)
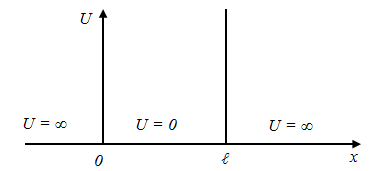
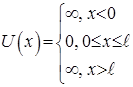
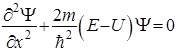
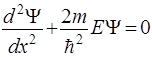
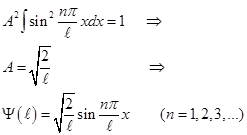

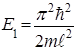
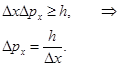

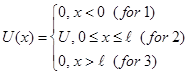
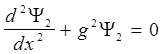

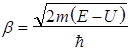


 classic ideas, which
classic ideas, which