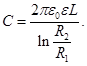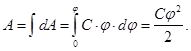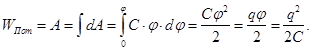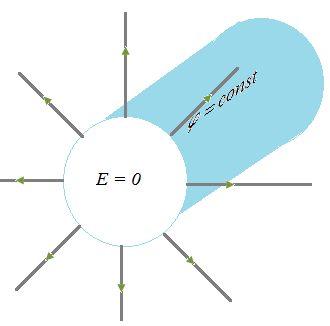
Conductors in electrostatic field

§ 1 of the The charge distribution in the conductor.

 Free charges in the conductor can move under the influence of an arbitrarily small force. Therefore, for the balance of the charges in the conductor must meet the following conditions:

1. Field intensity inside the conductor must be zero , since  
2. ie potential within the conductor must be constant.

Consequently, the surface charge of the conductor at equilibrium is an equipotential.
At equilibrium, the charges in any place inside the conductor can not be excess charges - they are distributed over the surface of a conductor with a density σ.

Consider a closed surface in the form of a cylinder whose generators are perpendicular to the surface of the conductor. On the surface of the conductor are free charges with surface density σ.

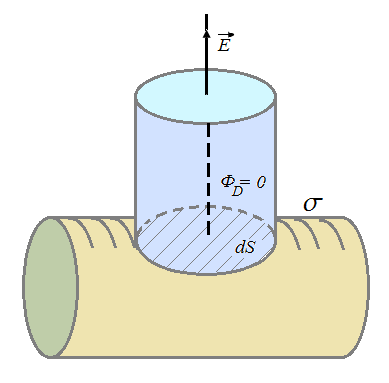
Because inside a conductor there are no charges, the flow  through the surface of the cylinder inside the conductor is zero. The flow through the top of the cylinder outside the a conductor on the Gauss theorem is equal

ie electric displacement vector equal to the surface density of free charges of a conductor or

  II. In making an uncharged conductor to an external electrostatic field his free charges will move: positive - on the field, negative - against the field. Then on one side of the conductor will accumulate positive and the other negative charges. These charges are said to be induced. The redistribution of the charges will be as long as the intensity in the conductor becomes zero, and the line intensity outside of the conductor will be the perpendicular to the surface. Induced charges appear on the conductor due to the displacement, ie are surface density charges and shifted as  is therefore  called the electric displacement vector.

§ 2 Capacitance conductors.

Capacitors

From experience, it follows that different conductors, being equally charged Q₁ = Q₂ takes various potentials φ₁ ≠φ₂ due to the different shapes, sizes, and surrounding environment conductor (ε). Therefore, for an isolated conductor have the formula

,

where - capacity of secluded conductor. Capacity of the secluded conductor is equal to a charge q, give the conductor that changes its potential by 1 volt.
In the SI system capacity is measured in farads

Capacity of the ball

1. II. Capacity solitary conductors is very small. For practical purposes it is necessary to create such a device, which allows to store large charges at small sizes and capacities. Capacitor- device for charge storage and electrical power. The simplest capacitor consists of two conductors separated by a gap of air or dielectric (air - is also a dielectric). The conductors are called the plates of the capacitor, and their location in relation to each other are selected such that the electric field is concentrated in the gap between them. Under the capacity of the capacitor understood the physical value of C equal to the ratio of the charge q, accumulated on the plates, to the difference of potentials  between the plates.

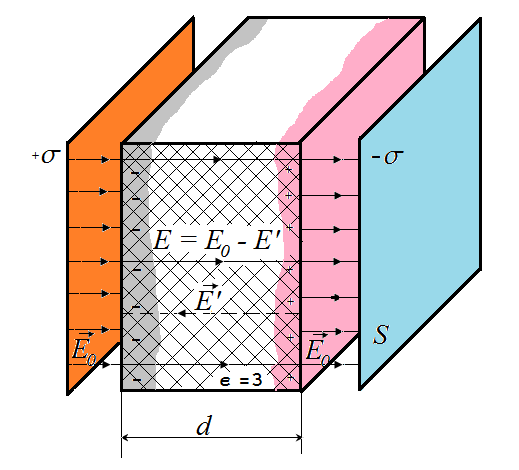
Calculate the capacity of parallel-plate capacitor with plates of area S, the surface charge density σ, the dielectric constant ε of the dielectric between the plates, the distance between the plates is d. The field intensity is

.

Using the relation Δφ and E, we find

 -

capacity of plate capacitor

For a cylindrical capacitor:

For a spherical capacitor:

Because for some values ??of the voltage in the dielectric breakdown occurs (electrical discharge through the dielectric layer), then there is a breakdown voltage capacitors. Breakdown voltage depends on the shape of facings, dielectric properties and its thickness.

III. Capacitance in parallel and series connection of capacitors

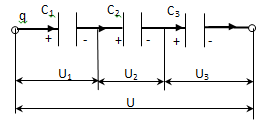
According to the law of conservation of charge

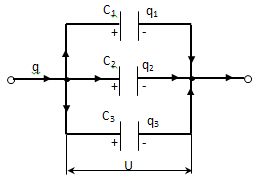
b) serial connection

According to the law of conservation of charge

§ 3 The energy of the electrostatic field

1. Energy of the system of fixed point charges

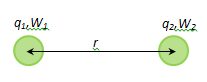
The electrostatic field is potential. The forces acting between charges - conservative forces. System of fixed point charges should have potential energy. We find the potential energy of two fixed point charges q₁ and q₂, separated by a distance r from each other.

Similarly, the potential energy of the charge q₁ in the field created by a charge q₂, equal to

It is seen that W₁ = W₂, then identify potential energy of the system of charges q₁ and q₂ in W, we can write

where φ_i - potential generated at the point where the charge q_i, all charges except the i-th.

1. The energy of secluded charged conductor.

The energy of the electric field of a charged secluded conductor can be determined by considering the total work done on the movement of small amounts of charge dq from infinity to this conductor.

To charge conductor from ground potential to a potential φ must do the work

The potential energy equal to the work that needs to be performed in order to charge the conductor

4. The energy of a charged capacitor.

because field is uniform inside the capacitor, you can enter the volume energy density (bulk density - the energy per unit volume)