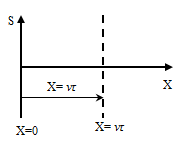ELASTIC WAVES

§ 1 the Waves in an elastic medium

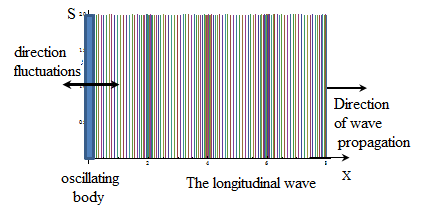
If the vibrating body (tuning fork, strings, membranes, etc.) is in an elastic medium, it leads to the oscillatory motion of a particle in contact with the environment, resulting in the body adjacent to this element of the medium, periodic

deformation (for example, compression and tension). In these strains in the environment appear elastic forces tend to return the elements of the environment to its original state of equilibrium, due to the interaction of neighboring elements of the environment, the elastic deformation will be transferred from one part of the environment to other, more remote from the oscillating body.
Thus, the periodic deformations caused in any place of the elastic medium, will be distributed in the environment with a rate that depends on its physical properties. The particles of the medium oscillates about equilibrium positions. From one part of the environment to another is transmitted only the state of deformation.

The propagation of the vibrational motion in the environment is called the wave process, or just wave. Depending on the nature of emerging with the elastic deformation distinguish longitudinal and transverse waves. In longitudinal waves, particles of the medium oscillate along the direction of oscillation. In transverse waves, particles of the medium oscillate perpendicular to the direction of propagation.

Liquid and gaseous media do not have elastic shear, so they are excited only longitudinal waves propagating in the form of alternating compressions and rarefactions. Waves excited on the surface, are transverse, they are due to the earth's gravity.

Suppose that a point source wave began excite vibrations in the environment at time t = 0, after a time t is the oscillation spread in different directions at a distance r = v_it, where v_i - wave velocity in this direction. The surface to which the vibration comes at some point in time is called the wave front. The shape of the wave front is defined by the configuration of the source of vibrations and the properties of the medium. In homogeneous media, the propagation velocity of the wave is the same everywhere. Medium called isotropic if the speed is the same in all directions. Wave front from a point source of oscillations in a homogeneous and isotropic medium has the form spheres, and such waves are called spherical.

In a heterogeneous and isotropic (anisotropic) environment, as well as from non-point sources of vibration wave front has a complex shape. If the wave front is a plane, and this form is saved as wave propagation in the medium, the wave is flat.

Surface waves, point of of which oscillate in the same phases, called wave or phase surfaces.

Graph showing the distribution in the medium fluctuating value at a given time is called the waveform.

§ 2 The equation of a plane wave

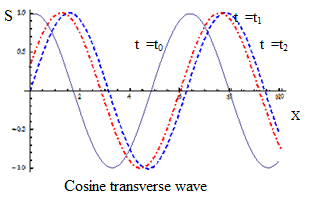
Let vibrations points lying in the plane x = 0, are due to the cosine law

Find the form of vibrations of points in a plane corresponding to an arbitrary value of x. In order to go from x = 0 to the plane wave needs time v –speed of wave propagation, therefore, the fluctuations of the particles lying in the x, will lag in time by τ of oscillations of the particles in the x = 0; ie, have the form

-

Equation of the incident, the traveling wave.

(equation of waves propagating in the direction of the axis X).

S-shift of the point of equilibrium in the plane at a distance x from the source of vibrations,
A - wave amplitude,

φ₀ - initial phase.

For a single wave can choose s and t, so that φ₀ = 0.

For several waves can not.

-

The equation of the reflected wave.

§ 3. The concept of the phase velocity.

Relation between the phase and group velocities

                                                                             (1)

It follows from it relation between the time t and the place's, in which the phase has a fixed value. Flows out of it value gives the rate at which the value is moving phase. Differentiating (1), we obtain

k - wave number, λ - wavelength.

Thus, the velocity v in the equation of the propagating wave is phase velocity, ie, it shows how fast spread phase of the wave (speed of the phase).

In all real wave processes have to deal with more complex waves with non-sinusoidal character. Such a complex wave can be represented as the sum of cosine or sine waves, or a group of such waves. In reality, there is the movement of groups of waves, each of which differs from the other in frequency. At any given time you can find the point at which there is a maximum vibration resulting overlay of these waves. At this point, any phase of the waves is the same. This point is called the center of the waves. The position of the center of the waves varies with time. This point corresponds to the maximum energy of the oscillating waves. The energy of the oscillating wave group moved at a speed equal to the speed of the center of a group of waves. This velocity is called the group velocity. It is denoted by u.

2. The link between the group and phase velocities.