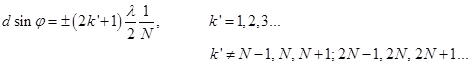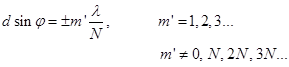§4 Fraunhofer diffraction on a single slit

length, b - width. The path difference between the beams 1 and 2 in the direction φ

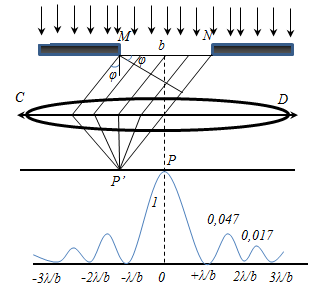
We divide the wave surface at the site MN gap on the Fresnel zone, having a form of bands parallel to the edge of the M slots. The width of each band is selected to the path difference from the edges of these zones is equal to λ/2, ie, in all on slit width go in    зон. zones. Because light is normally incident on the slit, the slit plane coincides with the wave front, so that all points in the plane of the front slot will vary in phase. The amplitudes of the secondary waves in the plane of the slit will be equal, as the selected Fresnel zone have the same size and equally inclined to the direction of observation.
Number of Fresnel zones  уfit the width of the gap depends on the angle φ.
Minimum condition for Fresnel diffraction:

or

then in point P is observed diffraction minimum.

Maximum condition:

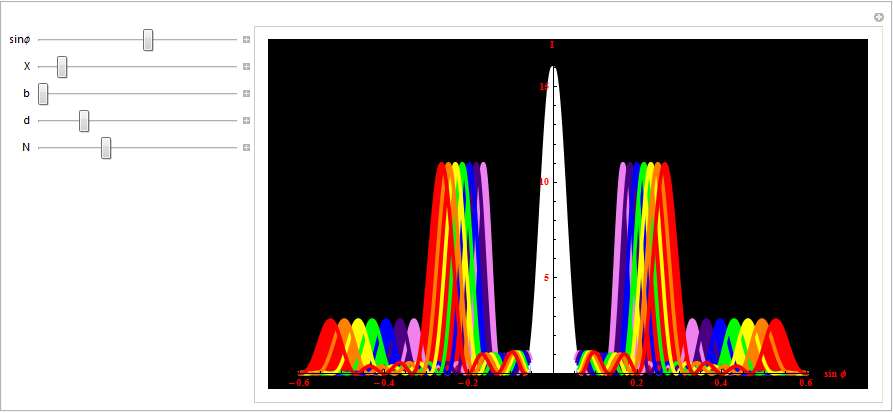
is observed diffraction maximum.

in the gap fits one Fresnel zone and, therefore, in point P the main (center) a maximum of zero order.

The main part of the light energy is concentrated in the main maximum: m = 0:1:2:3 ...; I = 1: 0.047: 0.017: 0.0083 ... (m-high order; I-intensity).

The narrowing gap leads to a broadening of the main peak and a decrease in its brightness (the same with the other peaks). With the broadening of the gap (b > λ) peaks will be brighter, but the diffraction bands are narrower, and the number of bands themselves - more. When b >> λ in the center of the source image is sharp, ie have the rectilinear propagation of light.

When falling of white light is decomposed into its components. While violet light will deviate less blue - more, etc., red - maximum. The main maximum in this case will be white.

§5 The diffraction grating

The diffraction grating is a collection of a large number N of identical width and parallel slits separated by opaque intervals, of the same as the width.                                 

b -width of the gap;

а - the width of the opaque area;

d = a + b -period or lattice constant .

The diffraction pattern on the lattice is defined as the mutual interference of the waves coming from all the cracks, ie a diffraction grating is multipath interference. Because slits are separated by the same distance, the differences of the rays coming from the two adjacent slots will be for the direction φ are identical across the entire grating .

                                                         (1)

In areas in which there is a minimum of one slit, and minimums will be in the case of N slots, ie the condition of the primary minimum of the diffraction grating is analogous to the condition for the minimum gap:

                                               (2)

-

the condition of the primary minimum.

                                                (3)

These peaks are located symmetrically relative to the center (zero k = 0) maximum.
For those angles φ, which is performed at the same time (2) and (3) the maximum will not, and will be a minimum (eg, d =2b for all even k =2р, р = 1, 2, 3...). Between the main peaks are additional very weak peaks, the intensity of which is much less than that of the main peaks (1/22 the intensity of the nearest main maximum). Additional peaks is N - 2, where N - number of strokes.

Between the main peak will be located (N - 1) additional minima.

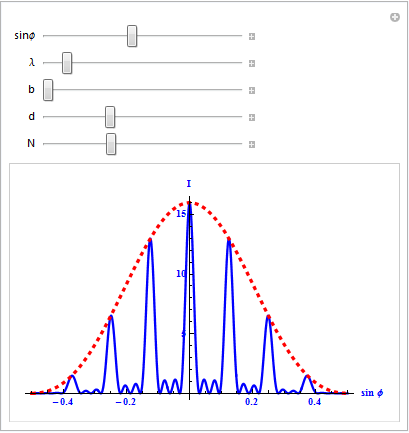
Thus, the diffraction pattern, at the diffraction on grating depends on N and the ratio d/b.
Let N =5, d/b =4. Then the number of major peaks (sin φ = 1) k_max < d/λ. Between them on the N - 2 = 3 additional maxima and N – 1 = 4 additional minimum. When k/m = d/b =2,4,8...  - the main maxima will not, and will be the primary minimum.
Thus, the diffraction pattern with diffraction on grating will be:

If the the diffraction grating  light up a monochromatic white light, the image will be shown in Fig. If illuminated with white light, all peaks except center (k = 0) decompose in the range - a set of component colors, and purple lines are closer to the center and red on (because λ_v < λ_r then φ_r < φ_v).