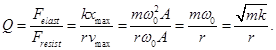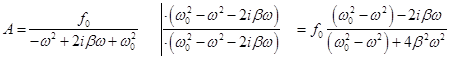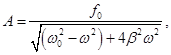Damped oscillations. Damping rate. Logarithmic decrement. Quality. Forced oscillations. Resonance. Resonance curve.

main

To the list of lectures

§6 Damped oscillations

Damping rate. Logarithmic decrement.

Quality

Free vibrations of engineering systems in the real world takes place when they are forces of resistance. The effect of these forces leads to a decrease in the amplitude of the fluctuating value.

Fluctuations with amplitude due to energy losses of real oscillating system decreases over time are called damped.

The most common cases where the resistance force is proportional to the velocity of the motion

where r - coefficient of resistance of the medium. The minus sign indicates that the

F_r is directed in the direction opposite the velocity.

We write the equation of vibrations at the point oscillating in a medium whose resistance coefficient r. According to Newton's second law

where β - coefficient of damping. This ratio describes the rate of damping. In the presence of the forces of resistance the energy of the oscillating system will gradually decrease, the oscillations are damped.

- Differential equation of damped oscillations.

-The equation of damped oscillations.

ω –- the frequency of the damped oscillations:

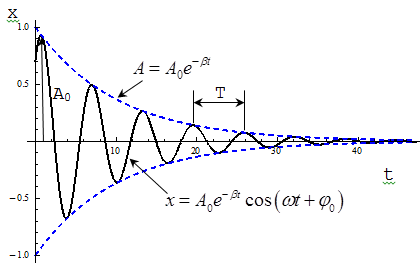
The period of the damped oscillations

Damped oscillations in the rigorous treatment are not periodic. Therefore, the period of damped oscillations can say when β is small. If you are weak damping (β→0), then

Damped oscillations can be considered as harmonic oscillations whose amplitude varies exponentially

In equation (1) A₀ and φ₀ - arbitrary constants that depend on the choice of the point in time at which we consider vibrations.

Consider the oscillations for at some time τ, for which the amplitude is reduced by a factor e

τ - relaxation time.

The damping coefficient β is inversely proportional time, during which the amplitude is reduced by a factor e. However, the damping factor is not enough to describe the damping vibrations. It is therefore necessary to introduce this feature for vibration damping, which includes the time of one vibrations. This characteristic is the decrement (in Russian: decrease) damping D, which is the ratio of the amplitudes, which are separated in time by a period:

Logarithmic decrement is equal to the logarithm of D:

Damping constant is inversely proportional to the number of vibrations that result in decreased amplitude of e. Damping constant - constant for a given system magnitude.

Another feature of the system is the vibrational quality factor Q.

Quality factor is proportional to the number of vibrations committed system during the relaxation time τ.

Quality factor Q vibrating system is a measure of relative dissipation of energy.

Quality factor Q oscillating system is a number indicating how many times the force of elasticity greater resistance forces.

The higher the quality factor, the slower the damping, the damped oscillations close to free harmonic.

§ 7 Forced oscillations.

Resonance

In many cases there is a need for systems that commit sustained oscillations. Get undamped oscillations in the system can compensate for the loss of energy when, acting on a system of periodically changing force.

Let

We write the expression for the equation of motion of a particle undergoing harmonic oscillatory motion by the driving force.

According to Newton's second law:

(1)

Differential equation of forced oscillations.

This differential equation is linear inhomogeneous.

His solution is the total solution of the homogeneous equation and a particular solution of the inhomogeneous equation:

We find a particular solution of the inhomogeneous equation. To do this, we rewrite (1) as

follows:

(2)

The particular solution of this equation sought in the form:

Then

In (2):

because holds for any t, we must have γ = ω, hence

This complex number is conveniently written as

where A is defined by (3 below), and φ - by the formula (4), therefore, the solution (2) in the complex form is

Its real part is the solution of equation (1) is:

Where

(3)

(4)

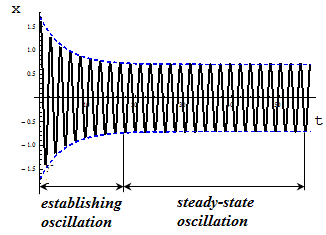
X_{t h} term plays a significant role only in the initial stage of the establishment of

Gig2 of oscillations as long as the amplitude of the forced oscillations reaches the value defined by equation (3). In steady state forced oscillations occur with a frequency ω and are harmonic. The amplitude (3) and phase (4) induced oscillations depend on the frequency of the driving force.
At a certain frequency of the driving force amplitude can reach very high values. The sharp increase in the amplitude of the forced oscillations in the frequency of the driving force to the natural frequency of the mechanical system, called resonance.

Frequency ω of the driving force at which a response is called resonance. In order to find the value ω_res need to find the condition of the maximum amplitude. To do this, you need to determine the minimum condition of the denominator in (3) (ie the study (3) on the extreme)

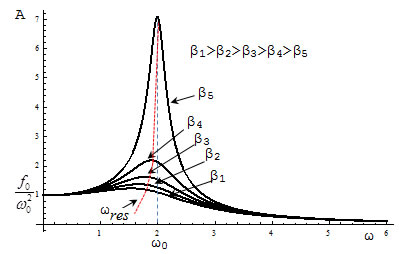
res curve

The amplitude of the fluctuating value of the frequency of the driving force is called the resonance curve. Resonance curve will be higher, the lower the damping factor β and decreasing β, the maximum resonance curves mixed right. If β = 0, then

ω_res = ω₀.

When ω → 0, all the curves come to value

- static deflection.

Parametric resonance occurs when the periodic variation of one of the parameters the system leads to a sharp increase in the amplitude of the oscillating system. For example, the cockpit, making "sun" by changing the position of the center of gravity of the system. (Same as in "boat".) See § 61. T 1 Savelyev I.V.

Self-excited oscillations are those vibrations whose energy is periodically updated by the impact of the system due to a power source in the same system. See § 59 v.1 Savelyev I.V.