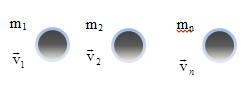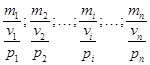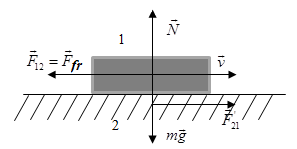
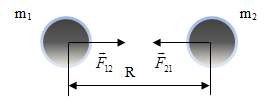
§ 3 Newton's Third Law

Every action of the body to each other is in the nature of interaction: if the body 1 acts on the body 2 with a force F₂₁, then the body 2 acts on the body with the force of one F₁₂.
Newton's Third law: the forces that act on each other interacting bodies are equal in magnitude and opposite in direction. (Action force equal to the force of the reaction).

Newton's III law is not always valid. It is strictly valid in the case of contact interactions, as well as the interaction of some distance from each other stationary bodies.
III of Newton's law that in any mechanical system geometric sum of all internal forces exactly equal to 0

IV. The law of gravity: Two point bodies attract each other through space with a force directly proportional to the two masses and inversely proportional to the square of the distance between them

γ - the gravitational constant (numerically equal to the force of mutual attraction 2 material points of unit mass at a distance of 1 m).

§ 4 The law of conservation of momentum

Consider a system consisting of n material points interacting.

The forces of interaction between the bodies that make up the system, let f_k. Interaction of external forces from the body not in the file system on the i body system denoted F_i.
We write Newton's II law applied to all bodies that form the system:

On Newton's third law:

Vector sum of the momenta of all bodies forming this system is called the resultant momentum of the system.

If external forces no effect on the body system (no interaction between bodies within the system and external bodies), or the action of external forces is compensated, then the system is called a closed or isolated.
In this case,

The law of conservation of momentum:
geometric (vector) sum of the momentum of a closed system remains constant over time in all interactions within the system:

LCM: 

that is, the interaction between the bodies of the pulses of individual bodies can vary in magnitude and direction, but within a framework that the vector sum of the momenta of all the bodies that make this system remains constant.

Example 1: A perfectly elastic collision

LCM:                                                

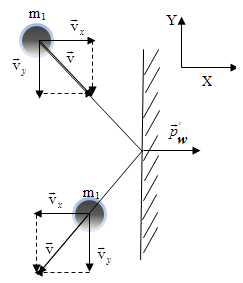
The projection on the axis of x:        

Example 2: An elastic ball hit on a fixed wall