§ 2 of the Fresnel zone.

The straightness of light

Evaluation of the integral formula (2) is generally difficult. Fresnel solved the problem of finding the amplitude in point P, replacing integration by summation, ie switched from continuous sums () to digital (Σ).

A point source S generates a spherical wave. Required to determine the amplitude of vibration waves in the in point P. Wave surface at a point O on the sphere will be. Fresnel proposed to split it into annular zones (sectors) so that the distance from the edges of each zone to point P is different on λ/2. Thus constructed sector areas called zones Fresnel.
Waves coming in point P from similar points of two neighboring zones have opposite phases, as path difference between the waves is λ / 2.

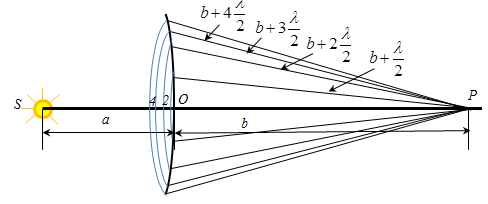
Is not too large m (m - number of zone), the area of the Fresnel zones are approximately equal S₁= S₂ =S_m. With the increasing number of the zone m distance increases b_m, from zone to point of P and the angle φ between the normal. to the elements of the zone and the direction to point of P. Then by (1) the amplitude of fluctuations Am excited m-th-zone in point P, decreases monotonically

А₁ >A₂ >A₃ >A_m >…>A_∞.

Because waves from two adjacent areas come in point P in opposite phase, they cancel each other, and then the resulting amplitude in point P is

А_рез = А₁ -A₂ +A₃ –A₄+…

Because A_m decreases monotonically, we can assume

And А_res can be written as

If the wave front is completely open, the number of zones m → ∞ and

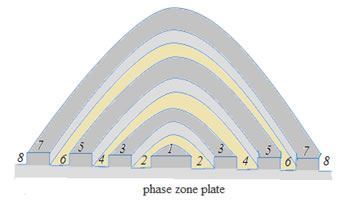
Amplitude, created at some point P across the surface of a spherical wave is half the amplitude of the first zone. Consequently, the distribution of light from S to P is as if the light output is distributed in a very narrow channel along the SP. that is straightforward.

Zone plates are used to enhance the intensity of light in the so-P by the overlap of even (or odd) Fresnel zones - amplitude zone plates, or changes on phase of the wave on π, passing through the thicker-even (odd) parts of the plate - phase zone plates.                

If the paths of light waves to put a screen with an opening into which is placed an even number of Fresnel zones, in point P is a minimum - light loss:

If the hole is laid odd Fresnel zones, in point P is a maximum - light amplification

3 the Fresnel diffraction

Fresnel diffraction or diffraction of spherical waves is, if the diffraction pattern is observed at a finite distance from the obstacle.

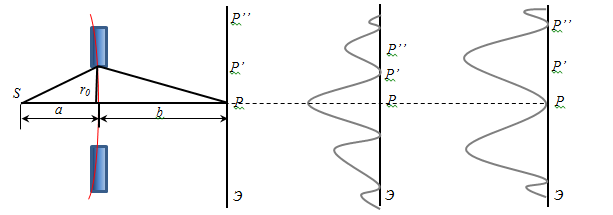
r₀ –the radius of the hole.

at r₀ <<a, b

therefore, the number of zones that fit into  the hole, will be:

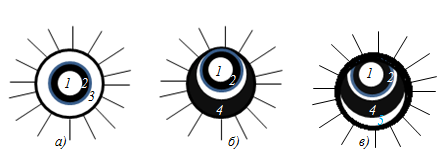
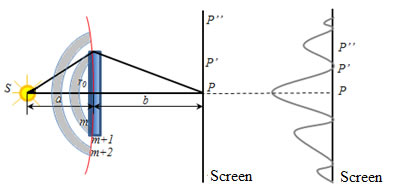
If m - odd, then, point P is maximum if m - even, in the p. P - minimum. Suppose point P is open for three Fresnel zone (Fig. a). If you shift the screen in point P ', the third area is partially closed and then partly opens 4th zone (Fig. b), therefore, point P' is a reduction of the amplitude. If the shift in the p. P ", then partially closed the 2nd and 3rd zone, but will except the 4th also 5th Zone (Fig. c), therefore, point P'' is light amplification.

Thus, the diffraction pattern of a circular aperture is given by alternating light and dark rings, the center will be a bright spot (maximum) if the hole contains an odd number of Fresnel zones (Fig. g), or dark, if fit even number Fresnel zones (Fig. g). If the screen is moved away SP line, then it will be an alternation of Fig. e and Fig. f.

If m <1, then the screen will be blurred bright spot.

2. Diffraction on disk

Let disc closes the m first Fresnel zones. Then the amplitude of the resulting oscillation in point P

Therefore           

ie in the point P observed interference maximum (bright spot). If you shift the screen in point P', then closes part of (m +1)-th zone, but will opens part (m +2)-th zone. Consequently, in point P' is a minimum (dark ring). As we move in point P" part overlaps (m +2)-th zone and simultaneously opens a part (m +3)-th zone, therefore, point P" is maximum. Thus, the diffraction pattern on a round disk has the form alternating light and dark concentric rings. In center is always put a bright spot.