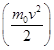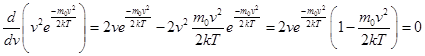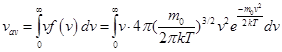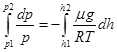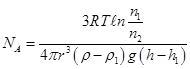§4 Maxwell's law of distribution of velocities and energies

The distribution law of ideal gas molecules in velocity, theoretically derived by Maxwell in 1860 determines how many molecules dN homogeneous (p = const) monatomic ideal gas of the total number N of molecules per unit volume at a given temperature T speeds in the range of inmates v to v + dv.

To derive the function of the velocity distribution f(v) equal to the ratio of the number of molecules dN, the speed of which lie in the interval v ÷ v + dv to the total number of molecules N and the size of the interval dv

Maxwell used two sentences:

a) all directions in space are equivalent and therefore any direction of the particle, ie, any direction of the velocity is equally likely. This property is sometimes called the property of the isotropic distribution function.

b) moving along three mutually perpendicular axes that are independent, ie x-component of velocity v_x does not depend on what the meaning of its components or v_y, v_z. And then the output f(v) is initially for one component v_x, and then extended to all the coordinates of speed.
It is also believed that the gas consists of a large number N of identical molecules are in a state of random thermal motion at the same temperature. Force fields do not apply to gas.
Function f (v) determines the relative number of molecules dN (v) / N speeds are in the interval from v to v + dv (eg gas has N = 106 molecules, with dN = 100 molecules have a velocity of v = 100 and v + dv = 101 m /s (dv = 1 m / s) then

Using the methods of probability theory, Maxwell found the function f (v) - the distribution of ideal gas molecules in velocity:

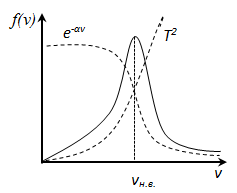
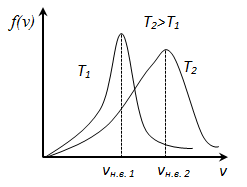
f (v) depends on the type of gas (the mass of the molecule) and the state variable (temperature T)
f (v) depends on the ratio of the kinetic energy of a molecule corresponding to selected speed vto the value of kT characterizes the average thermal energy of the gas molecules.

For small v  and the function f(v) changes almost on a parabola v². With an increase in the factor  decreases faster than the multiplier , ie a max function f (v). The speed at which the distribution function of molecules of an ideal gas at the maximum speed is called the most probable velocity v_mp from the condition:

 - therefore, with increasing temperature the most probable speed increases, but the area of ??S, bounded by the curve of the distribution function remains unchanged, since the normalization condition  since the probability of a certain event is 1), so that the temperature distribution curve f(v) will stretch and fall.

In statistical physics, the average value of any quantity is defined as the integral from 0 to infinity, the product of the probability density for this value (statistical weight)

Then the arithmetic average velocity of the molecules

and integrating by parts received

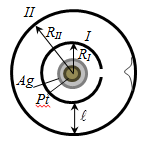
Speed, characterizing the state the gas

§ 5 Experimental verification of the Maxwell distribution law – Stern experience

Along the axis of the inner cylinder tight platinum wire, covered with a layer of silver, which is heated by the current. When heated, the silver evaporates; the silver atoms are emitted through the gap and onto the inner surface of the second cylinder. If both cylinders are fixed, all atoms regardless of their speed fall in the same place B. When rotating cylinder with an angular velocity ω silver atoms get into the points B ', B'' and so on. The magnitude of ω, the distance ? and displacement x = BB 'can calculate the velocity of the atoms belonging to a point B'.

Slit image getting blurred. Exploring the thickness of the deposited layer can estimate the distribution of the velocity, which corresponds to a Maxwellian distribution.

§6  Barometric formula. The Boltzmann distribution

Up to now, we have considered the behavior of an ideal gas not liable to attack to external force fields. From experience it is well known that the action of external forces, a uniform distribution of particles in space can be broken. Since gravity molecules tend to fall to the bottom of the vessel. Intense thermal motion prevents precipitation of, and the molecules are distributed so that their concentration gradually decreases with increasing height.

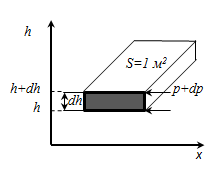
We derive the variation of pressure with height assuming that the gravitational field is uniform, the temperature is constant and the mass of all the molecules of the same. If the atmospheric pressure at a height h equal to p, then at a height h + dh is equal to p + dp (with dh> 0, dp <0, since p decreases with increasing h).

The pressure difference at the heights h and h + dh, we can determine as the weight of the air molecules enclosed in a volume with a base area equal to 1 and a height dh.

ρ - density at the height h, and since , then ρ = const.

Then

Of Mendeleev-Clapeyron equation.

Then

With the change in height from h₁ to h₂ pressure changes from p₁ to p₂

Potentiated this expression

Barometric formula shows how the pressure changes with altitude

At

Then

Because the

and

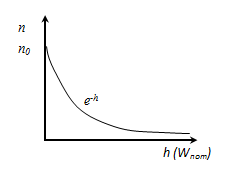
n - the concentration of molecules at a height

n₀ - the concentration of molecules at a height h = 0.

Because the

then

the potential energy of the molecules in a gravitational field

Boltzmann distribution law in an exterior potential field. From it follows that at T = const the density of gas is more there where potential energy of molecules is less.

§ 7 The experimental determination of the Avogadro constant

J. Perrin (French scientist) in 1909, studied the behavior of Brownian particles in the emulsion gamboge (tree sap) with dimensions were examined with a microscope, which had a depth of field - 1 mm. Moving the microscope in the vertical direction could be to investigate the distribution of Brownian particles in height.
Having applied to them a Boltzmann distribution law it is possible to write down

where m- particle mass

m₁ - weight of the displaced fluid.

If n₁ and n₂ concentration of particles at levels h₁ and h₂, and

then

Value  is in good agreement with the reference value,

 which confirms the Boltzmann distribution of particles.