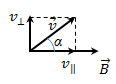|
§ 7 The motion of charged particles in a magnetic field
Lorentz force is
always perpendicular to the velocity of motion of a charged particle,
so it only changes the direction of the velocity without changing its
value. Consequently, the Lorentz force does not do work
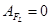 because because 
ie
static magnetic field does not do work on a moving charged particle in
it and the kinetic energy of the particle in a magnetic field does
not change.
 1. ie
static magnetic field does not do work on a moving charged particle in
it and the kinetic energy of the particle in a magnetic field does
not change. 1. ie
static magnetic field does not do work on a moving charged particle in
it and the kinetic energy of the particle in a magnetic field does
not change.  parallel to the vector parallel to the vector  , then sinα = 0°, FL = 0, and the particle moves in a rectilinearly inertia evenly. , then sinα = 0°, FL = 0, and the particle moves in a rectilinearly inertia evenly.
FL = 0; S=vt.
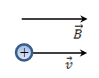
2. If the particle enters the magnetic field and the velocity vector 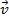 is perpendicular to the vector is perpendicular to the vector 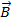 , thensinα = 90°, FL = qvB. Because , thensinα = 90°, FL = qvB. Because  perpendicular to the velocity perpendicular to the velocity 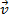 , then , then is
the centripetal force, and the motion of the particle will be in a
circle, the center of which coincides with one of lines of force
vector is
the centripetal force, and the motion of the particle will be in a
circle, the center of which coincides with one of lines of force
vector 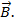
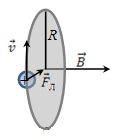 

.
- A charged particle enters the magnetic field at an arbitrary angle to the field lines vector
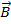 : : 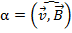 . A particle moves along a helix (spiral). In this case, the velocity of the particle can be decomposed into two components . A particle moves along a helix (spiral). In this case, the velocity of the particle can be decomposed into two components 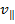 and and 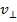 , and spiraling considered as the sum of two movements: the movement in a circle at a speed of , and spiraling considered as the sum of two movements: the movement in a circle at a speed of 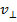 and linear motion along a force line and linear motion along a force line 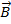 with speed with speed 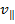 . .
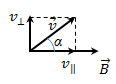 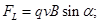 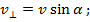 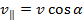 . .
Determine the radius and pitch of helix
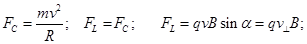
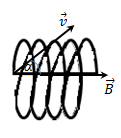 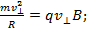
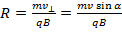 . .
The period of the spiral :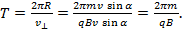
Pitch of helix: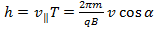
|