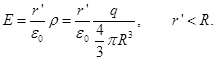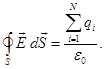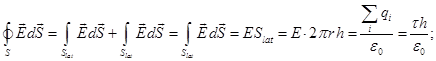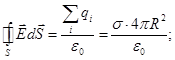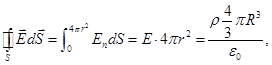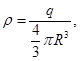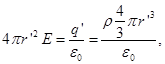|
§5 Flux of intensity
We define the flux of vector 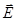 through any surface dS, through any surface dS, 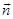 - normal to the surface, α - the angle between the normal and the force line of vector - normal to the surface, α - the angle between the normal and the force line of vector 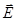 . You can enter a area vector . You can enter a area vector  . Flux of vector . Flux of vector 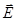  is called a scalar ФЕ equal to the scalar product of the intensity vector is called a scalar ФЕ equal to the scalar product of the intensity vector 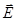 on the area vector on the area vector  . .
For a homogeneous field
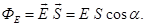
For inhomogeneous field
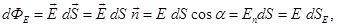
Where 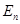 - the projection - the projection 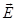 on on 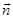 , , 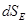 - the projection - the projection 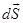 on the on the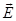
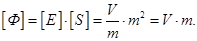
In the case of a curved surface S it must be broken down into elementary surface dS, to calculate the flow 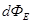 through the unit area, and the total flux is equal to the amount or limit of integrals of elementary streams through the unit area, and the total flux is equal to the amount or limit of integrals of elementary streams

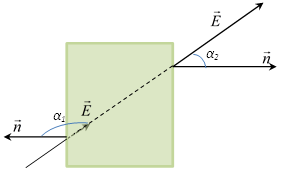 where where  - the integral over a closed surface S (eg, sphere, cylinder, cube, etc.) - the integral over a closed surface S (eg, sphere, cylinder, cube, etc.)
Flux  of of 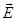 an algebraic value: not only depends on the configuration of the field an algebraic value: not only depends on the configuration of the field 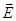 , but the destinations of your choice , but the destinations of your choice 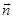 .
For closed surfaces, the positive direction of the normal is taken
outside the normal, ie, normal outward field covered surface. .
For closed surfaces, the positive direction of the normal is taken
outside the normal, ie, normal outward field covered surface.
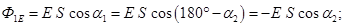

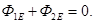
For a uniform field flow through a closed surface is equal to zero. In the case of inhomogeneous field
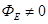
§ 6 Gauss's theorem and its application to the calculation of the electrostatic field
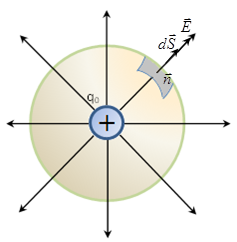
I. Consider the electrostatic field generated by a single positive charge. We include it in the sphere of radius R. We define the flow of intensity 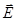 through a spherical surface of radius R. through a spherical surface of radius R.
 We divide the surface of the sphere S at the elementary area dS. The normal to the area dS is directed through the sphere of radius and coincides with the direction We divide the surface of the sphere S at the elementary area dS. The normal to the area dS is directed through the sphere of radius and coincides with the direction 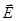 : : 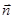 parallel parallel 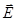 so so
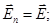
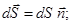 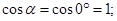   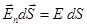
Then the flow of the vector 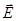 through the surface S is equal to the sum of flows through an area element dS and vanish dS we can write through the surface S is equal to the sum of flows through an area element dS and vanish dS we can write
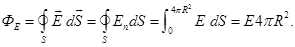
Considering that the field of a point charge is
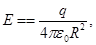
get
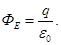
This result can be generalized to any surface.
Given the principle of superposition can apply our results to any number of charge inside the surface.
Gauss' theorem:
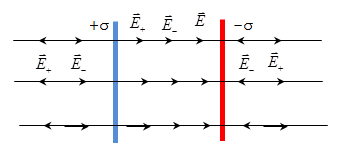
Flux of intensity  through an arbitrary closed surface is equal to the algebraic sum of the charges enclosed by this surface, divided by ε0 (ε0 - dielectric constant) through an arbitrary closed surface is equal to the algebraic sum of the charges enclosed by this surface, divided by ε0 (ε0 - dielectric constant)
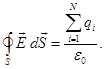
II. Application of the Gauss theorem.
- The field intensity created by an infinitely extended plane uniformly charged with surface charge density σ.
Surface charge density indicates which charge per unit area 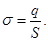
Lines of intensity  are perpendicular to the surface and sent from it on both sides. Construct a cylinder with a base S, whose elements of cylinde are parallel lines to intensity are perpendicular to the surface and sent from it on both sides. Construct a cylinder with a base S, whose elements of cylinde are parallel lines to intensity  . .
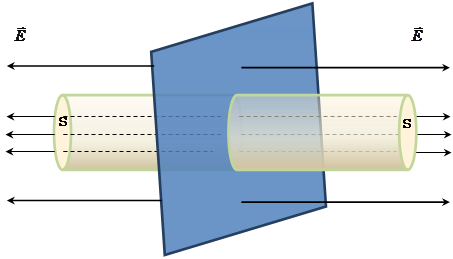
Since elements of cylinde is parallel to the lines of 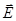  , the flow through the base of S is , the flow through the base of S is

The flow through the lateral surface of the cylinder is equal to zero, because 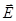 perpendicular S cosα = cos90 ° = 0, so perpendicular S cosα = cos90 ° = 0, so
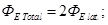
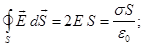 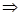

2. The field intensity created by two parallel infinitely extended plates with surface charge density + σ and -σ. We find the field E, using the principle superposition of the fields. In the region between the planes

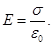
Left and right of the plane fields deducted as lines of intensity are directed toward each other  . .
3.
The field intensity created by an infinitely extended thread with linear charge density τ.
Linear charge density indicates which charge per unit length of the conductor
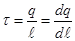
Required to determine the field intensity at a distance r from the filament. For this we construct a cylinder of radius r and height h, the axis of which passes the thread.
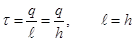

The flow through the base of the cylinder is considered zero, as perpendicular vector  and and  , therefore, the flow will be determined only flow through the lateral surface of the cylinder , therefore, the flow will be determined only flow through the lateral surface of the cylinder
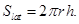
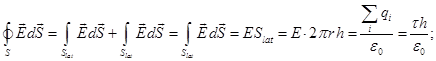
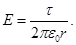
3. The field intensity generated by a spherical surface with a surface charge density σ.
On a sphere of radius R is distributed charge q. The surface charge density
 
ЛLines of intensity
are directed radially, moving away from the surface of the sphere at
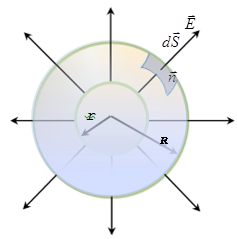
right angles. The surrounding area of ??this sphere of radius r and determine the intensity 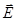
the flow through spherical surface of radius r.
When r > R the entire charge q is inside the sphere r. Then, by the Gauss theorem
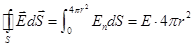 , becauseЕn = E. , becauseЕn = E.
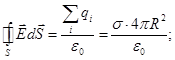
 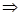 

When r < R, inside surface of radius r, and there are no charges so E = 0. Based on this screening - protection from external electric fields.
5. The field intensity of a body charged sphere with a volume charge density ρ.
The bulk density of the charge indicates which charge per unit volume
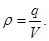
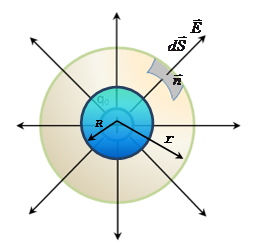 
a) For r> R, under item 4 to determine the
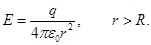
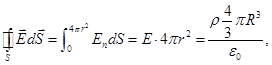

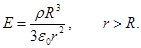
b) For r < R
 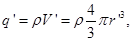
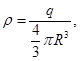
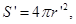
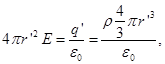
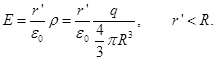
|