Spring pendulum. Elastic and quasi-elastic forces. The equation of a vibrating spring. Mathematical and physical pendulums. Periods of oscillation of mathematical and physical pendulum. Reduced length of a physical pendulum

main

To the list of lectures

§2 Spring pendulum.

Elastic and quasi-elastic forces.

The equation of a vibratingspring

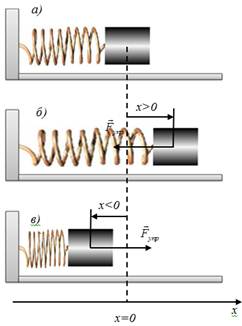
Consider a body of mass m, mounted on a spring with spring constant k (spring mass is neglected). Stretch the spring by x. Then Hooke's law on the body will act elastic force F_el

1. amount of force is proportional to the deviation of the system from equilibrium

2) direction opposite to the direction of the force displacement, ie force is always directed towards the equilibrium position (at х > 0, F_el < 0, при х < 0, F_el > 0)

3) In equilibrium х = 0 и F_el = 0.

On a Hooke's law

F_el = -kх.

System consisting of a material point of mass m and absolutely elastic spring with spring constant k, which may be free oscillations of the pendulum is called.
as a spring pendulum..

We write Newton's second law for Fig. b

then

and

If power is not in their nature elastic, but subject to the law F = - kx, it is called quasi-elastic force.

Obtain the equation of the pendulum. We take into account in the record of the second law of Newton, that

then

- differential equation point oscillates (differential equation of the pendulum).
Solution of differential equations:

- - oscillating point equation (the equation of a vibrating spring).

- - natural frequency of oscillations.

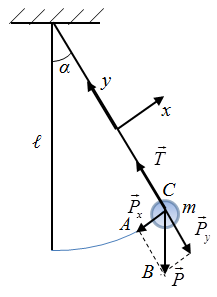
§3 Mathematical and physical pendulums.
Periods of oscillation of mathematical and physical pendulum

Mathematical pendulum - point mass suspended on a weightless inextensible thread, and oscillate in a vertical plane under the influence of gravity. Material point - a body whose mass is concentrated in the center of mass and size in terms of this problem can be neglected.

Mathematical pendulum at fluctuations is moved along a circular arc radius . His movement is subject to the laws of rotational motion.

The basic equation of rotational motion can be written as

(1)

M – themoment of forces, I – a moment of inertia, ε – a angular acceleration.

Resultant force and is equal to.

Of the triangle ABC

Thus, the oscillations of a mathematical pendulum occur under the quasi-elastic force - gravity.
Then (1) can be written as

(2)

The minus sign takes into account that the vectors and have opposite directions (the angle of rotation can be regarded as a pseudovector of angular displacement , the vector direction is defined by the rule of the right propeller, because of the minus sign is guided in the opposite side).

Having reduced in (2) on m and we will gain

At small angles of oscillations α = 5 ÷6° ,,we will gain

Label input

obtain the differential equation for the oscillations of a mathematical pendulum

Its solution:

-- the equation of a mathematical pendulum.

One can see that the angle α varies as the cosine . α₀ - amplitude, ω₀ - cyclic frequency, φ₀ - an initial phase.

- the period of oscillation of a mathematical pendulum
Physical pendulum - solid, vibrating by gravity around a fixed horizontal axis that does not pass through the center of gravity of the body, called the axis of oscillation of the pendulum.

The basic equation for the rotational motion of a physical pendulum is written as

At small angles of oscillation and the equation motion has the form

Then we put

get

-the differential equation of a physical pendulum .

-the period of oscillation of a physical pendulum

Equating T_Phys = T_mat: :

therefore, a mathematical pendulum with length

has the same period of oscillation, and this physical pendulum. - the reduced length of a physical pendulum - is the length of the a mathematical pendulum, the oscillation period coincides with the period of the physical