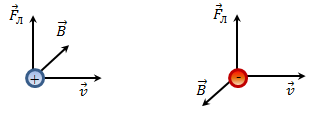main

To the list of lectures



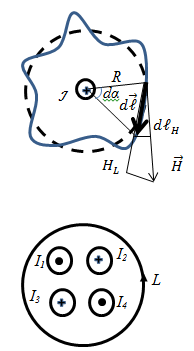
§ 3 the Law of the total current.

Vortex nature of the magnetic field

 

  1. Circulation of vector  (or ) in a closed loop is the integral over a closed contour L scalar product of vectors  (or )and ,where  - vectors of the unit length of the contour .

;

,

where –projection of vector  on vector .

;

;

.

Law of the total current:

Circulation of vector  an arbitrary closed loop is the sum of current covered by the circuit

;

.

Positive are those currents, the direction of which to the direction of passage of obeys the right hand rule. Currents, whose direction is opposite to bypass, taken with the minus sign.

.

  1. In contrast to the electric field, for which the circulation of the vector equal zero  and the electrostatic field is potential, the circulation of the magnetic field is not zero , if a path on which we consider the circulation covers currents. Field, the circulation of which is non-zero, is called a vortex or solenoidal. Consequently, the magnetic field is a vortex. In vortex field force lines are closed, therefore, there is no magnetic charges.

 

§ 4 A magnetic field the solenoid and toroid

 

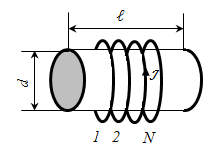
Solenoid is cylindrical shell, which are wound windings of wire. Consider an infinitely long solenoid, ie solenoid which ℓ >> d, where ℓ - length , d –diameter of the coil. Inside such a solenoid magnetic field is uniform. Uniform is a field, the field lines are parallel and their density is constant.

 

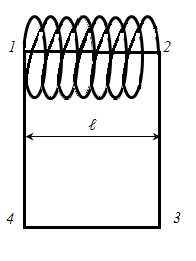
Apply the law of the total current to calculate the magnetic field of the solenoid. Represent the contour L, which is considered by the circulation of the vector , consisting of four related areas 1-2; 2-3, 3-4, 4-1. Then the circulation of the vector  the chosen us contour L is equal to

.

;

, because    and therefore , ,

,

because we have chosen the area 3 - 4 far enough from solenoid and one can assume that the

field far from the solenoid is zero,

, because   and therefore, .

Circuit L includes N currents, where N - number of turns the solenoid, then the law of the total

current

 ;

 -

- The magnetic field of an infinitely long solenoid

n - winding density - the number of turns per unit length

.

The field intensity inside the solenoid is equal to the number of turns per unit length of the

solenoid, multiplied by the current.

Toroid - torus, with coils wound on a wire. Unlike a solenoid, which has a magnetic field, both inside and outside, fully toroidal magnetic field is concentrated inside the coils, ie there is no dissipation of magnetic field energy.

,

where .

 –magnetic field of toroid.

if R >>Rturn, then R ≈r and H = nI.

 

§5 Ampere force

  1. Ampere studied the effect of magnetic field on the current-carrying conductors and found that the force , with which the magnetic field acts on the element wire  with current I,in a magnetic field , directly proportional to the current I and the vector product on the magnetic induction

 

 –

The Ampere force (or Ampere's law)

The direction of the Ampere force is situated by the rule of the vector product - on left-hand rule: four elongated fingers of his left hand placed on the direction of the current, vector  included in the palm, deflected at right angles to the thumb will show the direction of force acting on a current-carrying conductor. (You can also determine the direction of  with his right hand: turn the four fingers of the right hand of the first factor to second , thumb indicates the direction of .)

Module of Ampere force

,

where α –- the angle between the vectors  and        .

If the field is uniform, and the current-carrying conductor of finite size, the

,

.

At  perpendicular

.

 

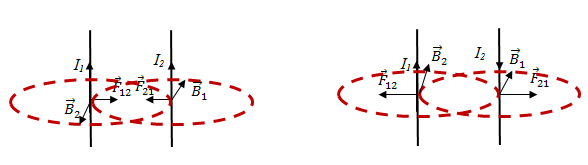
2. Definition of the unit of measurement of the current.

Any current-carrying conductor generates a magnetic field around itself. If you put it in the field of the other current-carrying conductor, the conductor between the forces of interaction. In this case, co-directional parallel currents attract each the opposite direction - are repelled

Consider two infinitely long parallel conductors with currents I1 and I2, in a vacuum at a distance d (for vacuum μ = 1). According to Ampere's law

.

A magnetic field of direct current is

,

then

,

the force per unit length of the conductor

.

The force per unit length of the conductor between two infinitely long conductor with a current directly proportional to the current in each conductor and inversely proportional to the distance between them.

           

Definition of the unit of measurement of the current - Ampere:

Per unit of current in the SI in place a DC current which is flowing in two infinitely long parallel conductors infinitesimal cross section, located in vacuum at a distance of 1 m from each other, is the force exerted per unit length of the conductor is equal to 2·10-7 N.

µ = 1; I1 = I2 = 1 A; d = 1 m; µ0 = 4π·10-7 H/m –magnetic constant .

Amper's .

 

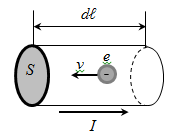
§6 The Lorentz force

Under the Ampere’s law, force acting on the current element , determined by the formula

.

Consider that the elementary current is none other than the directional movement of electric charges

,

where V –volume , n –the carrier density , j –current density , S –

cross-sectional area of the

conductor, e – electron charge (e = 1,6·10-19 C), dl -  the element length of the conductor,  –velocity of the electron motion .

;

;

.

Ampere force acting on the elementary current  can be seen as the resultant force of the all forces exerted by the magnetic field on each charge separately. Then, the force acting on a moving charge in a magnetic field, we find by dividing the number of Ampere charge in this volume element of the conductor

.

This force is called the Lorentz force:

.

 –module of the Lorentz force

The direction of the Lorentz force is determined by the left-hand rule: four fingers of his left hand - the speed, the vector  enters in the palm, deflected at right angles to the direction of the thumb shows the Lorentz force to the positive charge. For a negative charge - four fingers against the speed, then the same as for the positive charge.

To the list of lectures

main