Solid state physics devices

§1 Concept about a band theory of solid bodies

 It is known that the electron can be in an isolated atom on quite certain energy levels. These values of energy of an electron (or atom) term allowed. The allowed values of energy in atom are separated the wide fields of the forbidden energies. Let is available N isolated atoms. While atoms do not interacted, they have identical energy levels. The level occupation is carried out by electrons in each atom irrespective of filling of similar levels in other atoms. In process of approaching of atoms between them arise all amplifying interaction, leading to that energy levels are biased, splitted and dilated in bands, it is formed  so-called band an energy distribution. Instead of one  level identical to all N atoms arises N very close, but not conterminous levels, i.e. each level of isolated atom is splitted in a limit on densely located N levels forming a strip or a band.

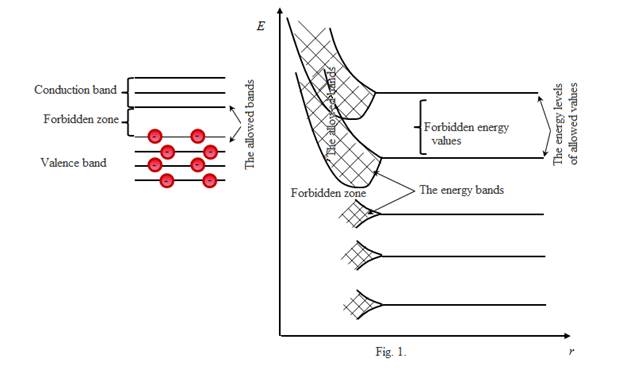
            From figure 1 it is visible that levels of the exterior valence electrons most feebly related to kerns and having the greatest energy, and also higher levels which in the basic state of atom are not occupied by electrons absolutely are considerably splitted and dilated only. Levels of inner-shell electrons or are not splitted at all (the nearest to a kern), or splitted feebly, i.e. in solid bodies inner-shell electrons behave the same as in isolated atoms, valence electrons are socialized (“collectivized") - belongs to all solid body.

            Formation an energy distribution on band in a crystal is quantum-mechanical effect and streams from an uncertainty relation of Heisenberg. In a crystal valence electrons of atoms are related more feebly to kerns and can transfer from atom to atom through the potential hills parting atoms i.e. to move without change of a total energy (tunnel effect). It leads to that the medial lifetime t of a valence electron in the given atom in comparison with an isolated atom essentially decreases and makes ~10^-15 s (for an isolated atom ~10^-8 s). Time of  life of electrons in any state are related to uncertainty of its energy (level width) an uncertainty relation hence if the natural breadth of spectroscopic lines makes∼10^-7eV in limits, DE»1÷10  i.e. energy levels of valence electrons are dilated in a band of the allowed values of energy.

            Each allowed band "contains" in itself so much nearby discrete levels, how many atoms the crystal contains. As a rule, crystals contain  atoms n~10²⁰÷10²⁵, hence, distances between the next electronic levels in a band makes ∼10^-22 eV.

            The allowed energy bands are parted by forbidden bands. Electrons cannot be in forbidden bands.

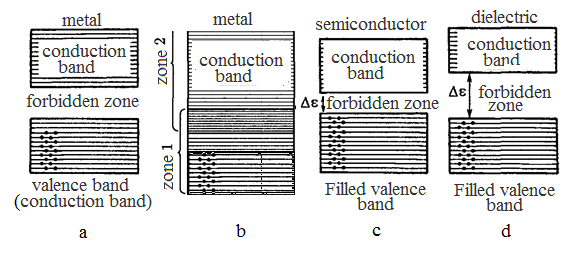
§2 Metals, dielectrics and semiconductors

in a band theory

            From the point of view of a band theory distinction of electronic properties of metals, dielectrics and semiconductors speaks two parents: 1) character of an arrangement of energy bands, is more exact in breadth of a forbidden band 2) various filling with electrons of the allowed energy bands.

            Depending on a degree of filling of bands electrons and forbidden band breadths are possible four cases:

The band formed by levels of energy on which there are valence electrons in the basic state of atom, is termed as a valence band.

 At absolute zero valence electrons fill in pairs inferior levels of a valence band.

            The conduction band - is formed by energy levels, being on which electron is generalized, i.e. not related to separate atom (a band of free electrons). If in a conduction band there are electrons at the electric field appendix on substance the current will proceed.

            In metals (I) the valence band is not completely filled by electrons. To the electrons which are on the upper energy levels, it is enough to inform energy~10^-23 eV to transfer them on higher levels, to make free. Energy of a thermal motion (kТ) makes at 1 К quantity of the order 10^-4 eV, i.e. at " (any) temperatures there are free electrons and such solid body will be a conductor, i.e. in metals (I) the valence band is partially filled and is a conduction band. In metals (II) conduction band is overlapped with a valence band. In this case the wide "hybrid" band with which valence electrons fill only partially is formed. Above the occupied levels vacant levels and such solid body are located, as well as in a case (I) will be a conductor.

            The band theory of solid bodies has allowed to explain, why electroconductivity does not increase with magnification of valence of metal as it follows from the kinetic theory. Al³⁺, hence, has 3 valence electrons, i.e. conductivity under the classical theory should be more than at Cu¹⁺ (1 valence electron). From the up-to-date point of view the electrical conductivity depends not on number of valence electrons, and from number of electrons  for which in the upper conduction band there is a sufficient number of the free energy states.

            Divalent metals have some number of the free energy levels in a conduction band. But number of electrons which can be transferred an exterior electric field in the free states less, than at monovalent metals. Even less than such electrons at tervalent metals.

            At dielectrics (III) valence band  is filled completely, the forbidden band breadth is great (DE>3 eV) the thermal motion cannot throw an electron from a valence band in a conduction band. Only at the appendix of very strong electric fields electron transition in a conduction band (a dielectric breakdown is possible at the shorting voltages depending on a sort of a material and its thickness).

            At semiconductors (IV) valence band is filled completely. The forbidden band breadth is insignificant (DE ~1 eV). At temperatures ~200 – 300  °C or exterior actions (for example, light - an inner photoemissive effect) electrons transfer an irradiation from a valence band in a conduction band and after semiconductors the current proceeds.

Differences from the point of view of a band theory:

• Between metals and dielectrics

At 0 K metals in a conduction band have electrons, at their dielectrics are not present.

At metals is not present or very narrow forbidden band, at dielectrics - a major forbidden band.

• Between dielectrics and semiconductors:

Breadth of a forbidden band of the semiconductor ~1 eV; a dielectric >3eV.

At 0 K semiconductors behave as dielectrics, at increase of temperature conductivity of the semiconductor grows.

Concept the energy level or an energy band characterises only an energy  state of an electron, instead of its  geometrical arrangement in a body.