Two blocks of masses m1 and m2 are connected by a string of negligible mass which passes over a pulley of mass M and radius r mounted on a frictionless axle. The blocks move with an acceleration of magnitude a and direction as shown in the diagram. The string does not slip on the pulley, so the tensions T1 and T2 are different. You can assume that the surfaces of the inclines are frictionless. The moment of inertia of the pulley is given by I = A? Mr 2 : (a) Draw free body diagrams for the two blocks and the pulley. (b) Write down the equations for the translational motion of the two blocks and the rotational motion of the pulley. (c) Show that the magnitude of the acceleration of the blocks is given by a=g(sqrt(3m2-m 1)/(M+2(m2+m1))
Solution:
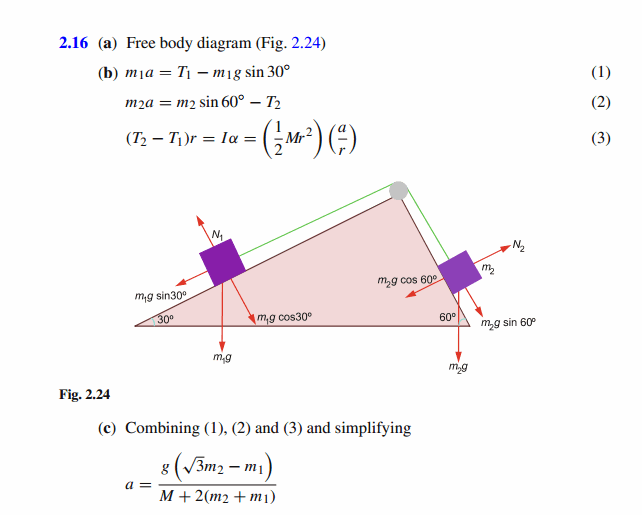
|

