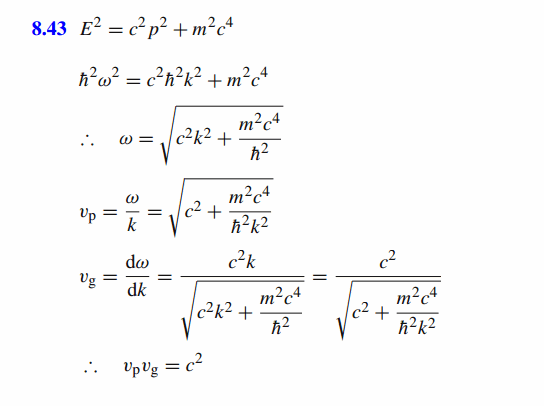
The relation for total energy E and momentum p for a relativistic particle is E^2 = c^2p^2 + m^2c^4 , where m is the rest mass and c is the velocity of light. Using the relations, E = hw and p = hk, where w is the angular frequency and k is the wave number and h= h/2pi , h being Planck's constant. Show that the product of group velocity vg and the phase velocity vp , vp·vg = c^2 .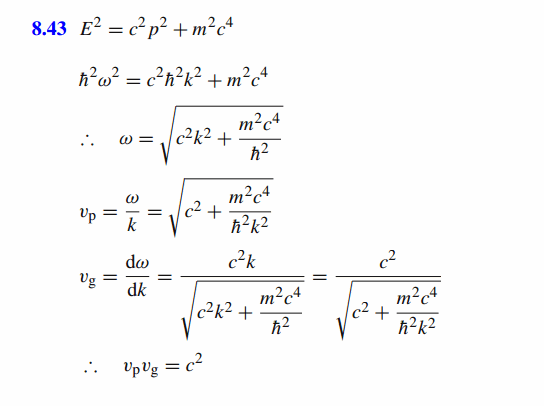 |
| New search. (Also 5349 free access solutions) |