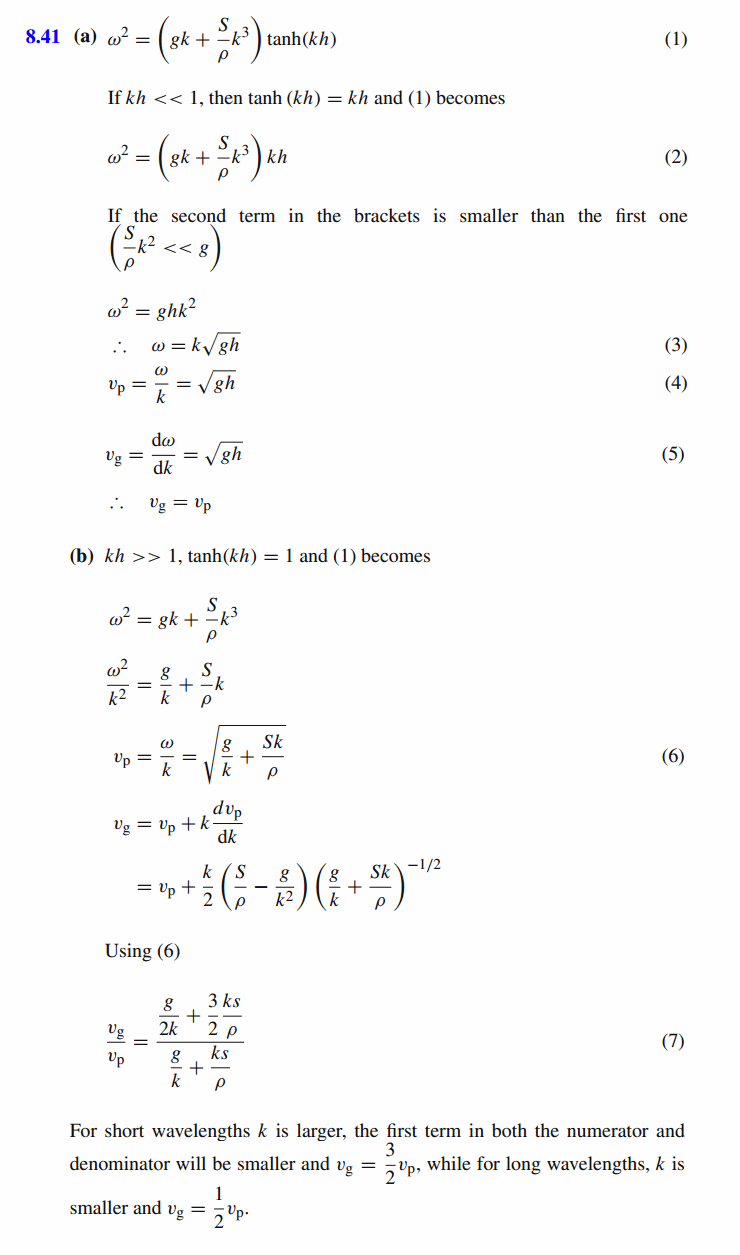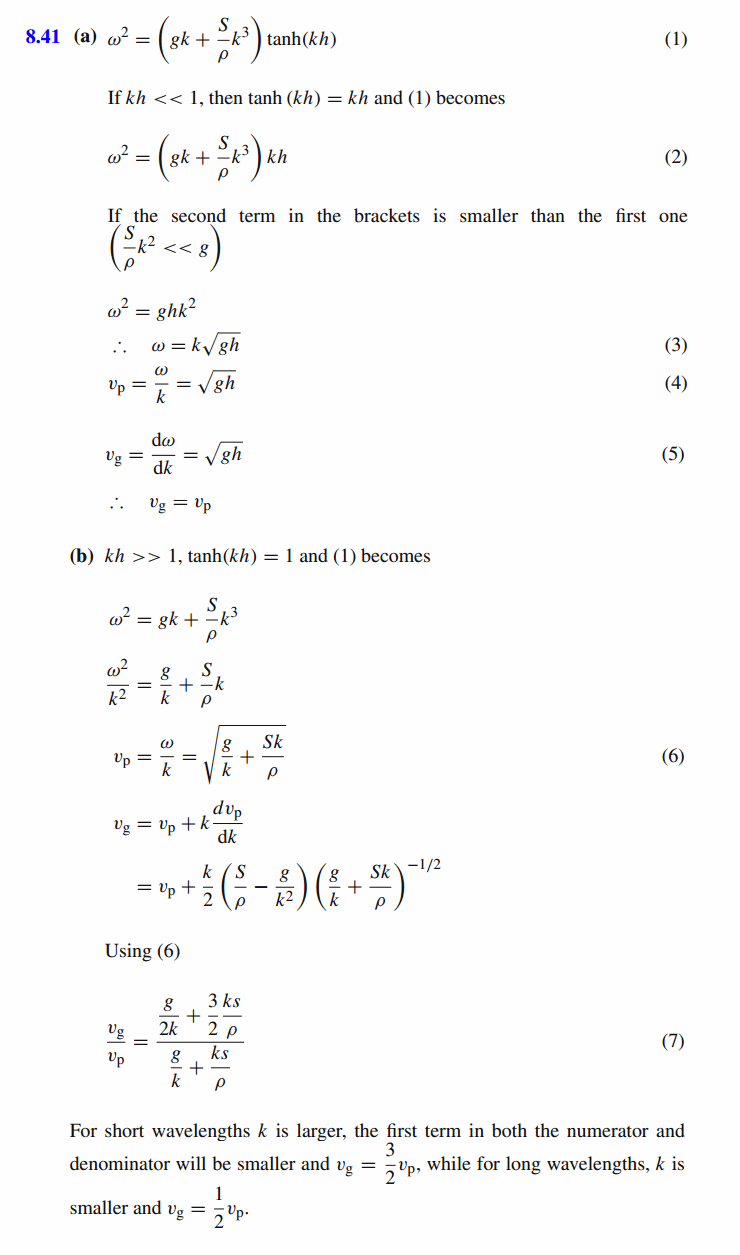The general dispersion relation for water waves can be written as w^2 = (gk + s/r k^3) tanh kh where g is acceleration due to gravity, r is the density of water, S is the surface tension and h is the water depth. Use the properties of tanh x function viz. for x >> 1, tanh x = 1 and for x << 1, tanh x = x . Show that (a) in shallow water the group velocity and the phase velocity are both equal to sqrt(gh if the wavelength is long enough to ensure that Sk^2/v = 4pi^2S/L^2s << g. (b) Show that for deep water the phase velocity is given by vp = sqrt(g/k + Sk/r) and find the group velocity.
Solution:
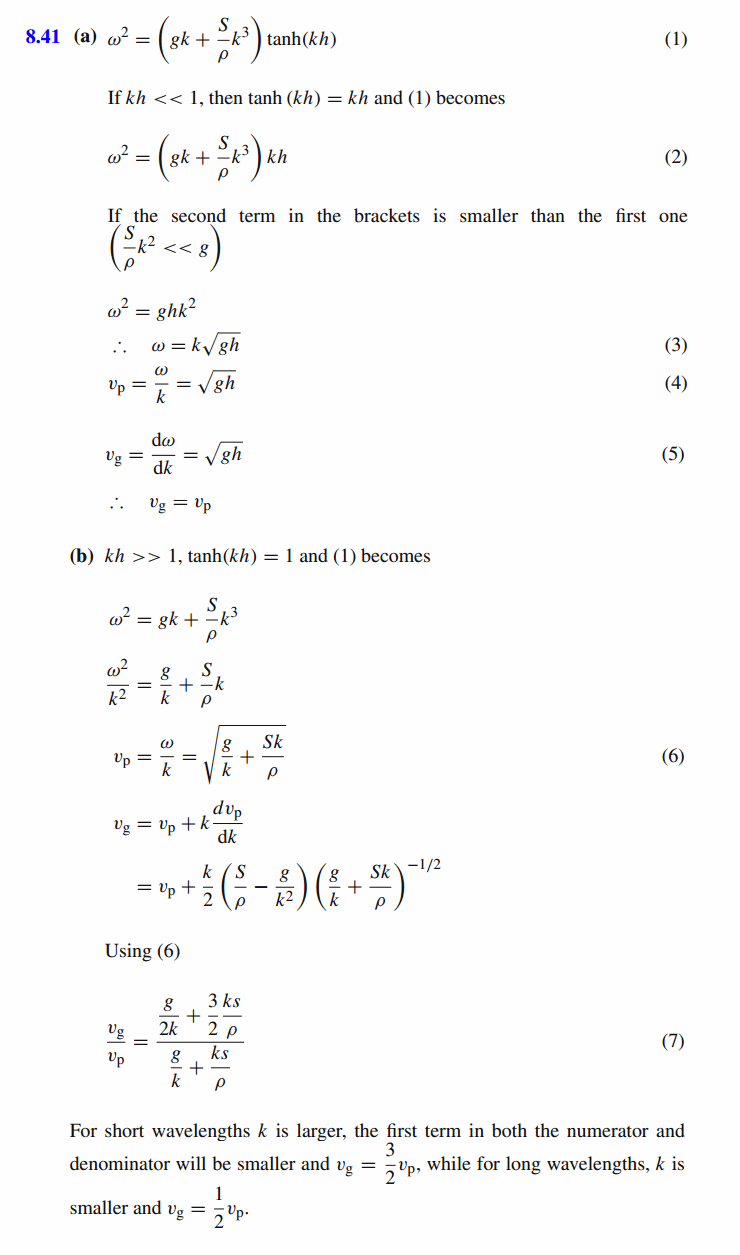
|