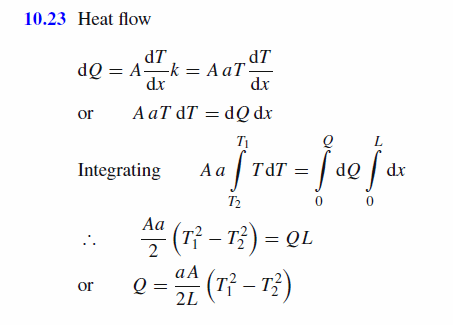
At low temperatures, say below 50 K, the thermal conductivity of a metal is proportional to the absolute temperature, that is, k = aT , where a is a constant with a numerical value that depends on the particular metal. Show that the rate of heat flow through a rod of length L and cross-sectional area A and whose ends are at temperatures T1 and T2 is given by Q = dA/2L (T1^2-T2^2 ).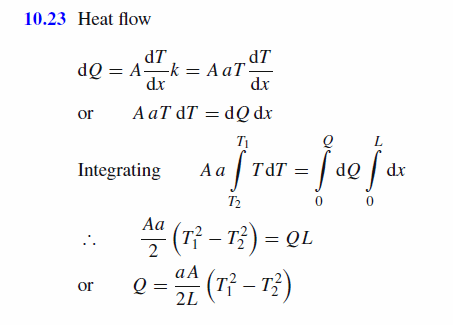 |
| New search. (Also 5349 free access solutions) |